- #1
jonjacson
- 447
- 38
Homework Statement
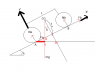
I´ll need an image to show the problem:
A bike with length L is on an inclined plane, the distance between the center of gravity and center wheel centers A,B is L/2.
Brakes are acting on the wheels so we have a static position.
In the picture is possible to see normal forces perpendicular to the plane Na,Nb, friction forces Fa,Fb and the gravity force acting at the CG point.
I have to calculate the value of the forces and moments on the system in order to get the equilibrium.
I´ll use the coordinate system X', Y' with origin A. And angle h, the lenghts L,f are known.
Homework Equations
Sum Fx= 0
Sum Fy=0
Sum Ma=0
The Attempt at a Solution
In order to calculate the moments I´ll need the moment arms. Since the reference point is A forces Na, Fa, Fb won´t be calculated since their moment arms are 0.
The gravity has a moment arm that I showed with a strong red line.
I´m going to calculate it:
Distance AZ= L/2 ; BZ=f/ tg (h) ; So the distance AB= L/2 - f/tg(h)
In the triangle AVB I see:
cos(h)=AV/AB----> AV=moment arm=cos(h)*AB
And the moment arm of the force Nb is simply L, finally:
Sum Ma= -mg*(cos(h)*(L/2- f/tg(h))) + Nb*L = 0
Sum Fx= Fa + Fb -mg sin(h)=0
Sum Fy= Na + Nb -mg cos(h)=0
And my problem is that I have three equations and four unkown quantities: Na, Nb, Fa, Fb.
Is this one of those cases of static indeterminacy?
Have I done any mistakes?
Maybe I should use a condition like Fa=Fb or Na=Nb but I can´t see any physical reason behind those conditions so I won´t use them. Experience tells me that Na will be higher than Nb on this inclined plane.
So I´m surprised, or I´m doing something wrong or it´s not possible to calculate this problem without any extra assumption, I´ll wait for your answers to check what´s happening here.
Thanks!