SUMMARY
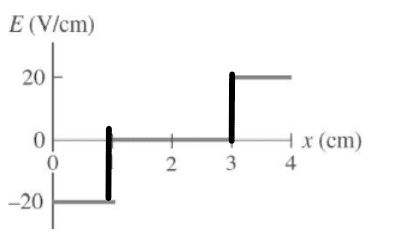
The discussion centers on the proper representation of discontinuous electric fields in graphing. Specifically, it emphasizes that vertical lines should not be drawn at discontinuities, such as at x = 1 cm and x = 3 cm, because this would incorrectly suggest that the electric field possesses all intermediate values. The correct approach is to plot the electric field as discontinuous functions to accurately reflect its behavior at these points. This clarification was provided by user @kuruman, reinforcing the importance of accurate graphing techniques in physics.
PREREQUISITES
- Understanding of electric fields and their properties
- Familiarity with graphing techniques for discontinuous functions
- Knowledge of basic calculus concepts related to continuity
- Experience with physics problem-solving methodologies
NEXT STEPS
- Research the principles of discontinuous functions in mathematics
- Learn about graphing electric fields and their characteristics
- Study the implications of continuity and discontinuity in physics
- Explore advanced graphing tools for visualizing electric fields
USEFUL FOR
Students and professionals in physics, educators teaching electric field concepts, and anyone involved in graphing mathematical functions related to physics.
 ,
,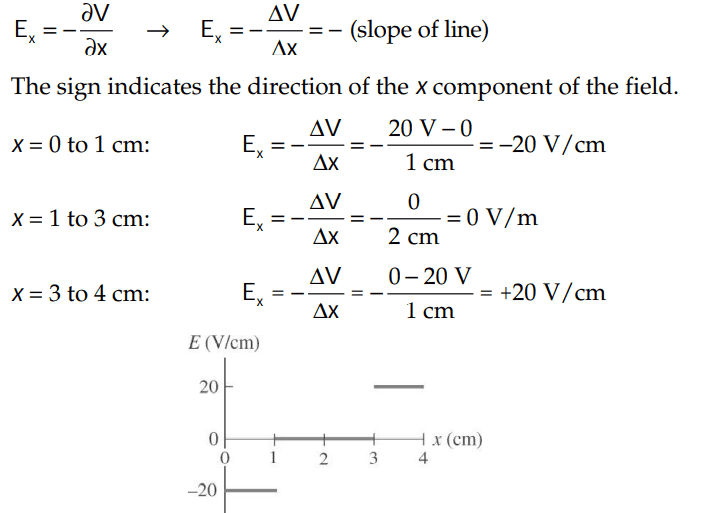
 ?
?