Dynamics, Newton's laws, Problem with free body diagram and work

[akmenio]

Homework Statement

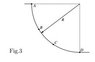
A boy skateboards down a curved playground ramp. If we treat the boy and his skateboard as a
particle of total mass m = 25:0 kg, he moves through a quarter-circle with radius R = 3:0 m. He
starts from rest at point A and there is no friction.
(a) Find his speed at the bottom of the ramp
(b) Draw free-body diagrams for points A, B, C and D.
(c) Find the normal force that acts on him at the bottom of the curve
(d) Find work done by the normal force

Homework Equations

E=mgh
E=(mv^2)/2

The Attempt at a Solution

I find answer for a, I use that change of potential energy is equal to kinetic. Also I done c because the normal force is equal change of potential energy. But i haven't got idea how to draw free-body diagrams and whywork done by normal force is equal 0 (Our teacher give us this answer)

 

[Doc Al]

I find answer for a, I use that change of potential energy is equal to kinetic.

Good.

Also I done c because the normal force is equal change of potential energy.

Not sure what you mean.

But i haven't got idea how to draw free-body diagrams

Just label the forces acting on the particle, indicating their direction.

and whywork done by normal force is equal 0

At any point along the path, how does the direction of the normal force compare to the direction the particle is moving?