physics_cosmos
- 6
- 0
Homework Statement
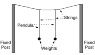
My problem/task is to explain in elementary terms the dynamics of a string coupled pendulum, the same as in this diagram:
Is it simple to make a free body diagram for the pendulums? Is it possible to understand the motion as being caused by SHM oscillation of the top horizontal spring from which the weighted pendulum are suspended?
Thanks in advance for any help with this problem.