Identity
- 151
- 0
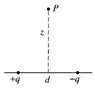
Say you have a charge distribution in the picture, and you want to find the potential THEN the electric field at P, using E = -\nabla V
I found the potential to be 0, and yet the field isn't. Why is this?
And how would we get the actual field from the voltage?
I found the potential to be 0, and yet the field isn't. Why is this?
And how would we get the actual field from the voltage?
Attachments
Last edited: