Easy university force/motion problem

[Optikspik]

1. A block with the mass m=2,0kg is dropped from 0,5 meters above an incline with an angle of 30 degrees. The incline stands on a table , as shown in the following picture. The table is 2 meters high. The friction is negligible.

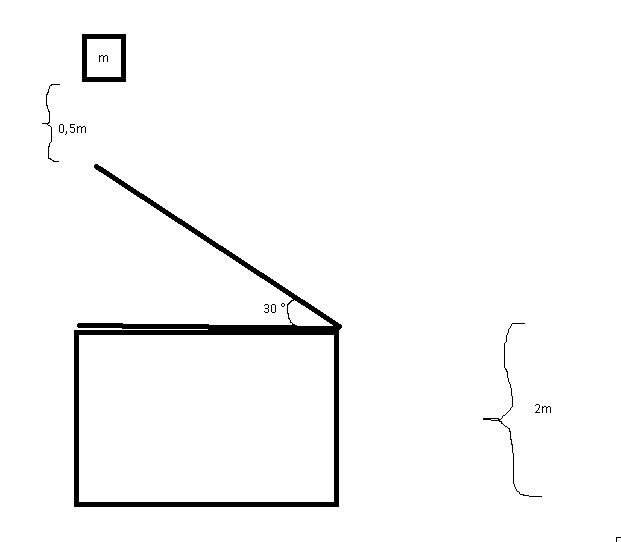a) Determine the acceleration of the block while sliding on the incline
b) Determine the v of the block when leaving the incline
c) How far from the table will it land
d) How long time does it take from the starting position until the block hits the floor.
e) Does the mass of the block play any role at all?

a) m_tot= 2kg
a=F/m

Since only the x composant of the weight (FG) will help the block accelerate
a=2*g*sin 0,3 / 2kg = g/2kg= 4,91 m/s^2
b) The first free fall gives v final from:

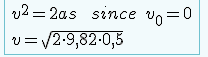
Hwwever, then I am stuck on how to continue on b ), i need to find s of the incline, or v final of the incline. Or do i need to put v-final as 0 and solve from it hits the incline until the floor, instead of making one calculation for just the incline?

 

[ogg]

Could the incline be 0.1 m long? Could the incline be 1000 m long? If so, then the problem statement is either incomplete or requires an equation rather than a value for the answer. (That is, the answer will be in terms of either the incline's length or height). Given the silly situation where you have to assume that the block magically hits the incline but neither bounces NOR gives up any energy to the table, I'd guess that the problem is what we call "ill-formed" - meaning the teacher screwed-up. What you could do, is use a ruler (or calipers, etc.) and assume the table is drawn exactly in proportion so that you could use the distance between the block's bottom and the top tip of the incline as being exactly 0.5 meters and all other distances are proportional (or use the 2.0 meter value...you could also compare the two 'coversion factors' you obtain to see how close they are to one another)

 

[haruspex]

Is the diagram your own, based on the textual information? If so, I suspect the 0,5m is supposed to be the height above the table, not the height above the top of the incline, making the length of the incline 1m.
If the diagram is right then as ogg says you need more information. You would also have to assume the block does not bounce; you would then use momentum conservation parallel to the incline to find its initial speed on the slope.

 

[Optikspik]

I miss understood the problem, but is this information enough to solve it?

 

[haruspex]

I miss understood the problem, but is this information enough to solve it?

Yes.

 

[Optikspik]

**** ME FPRGOT TRIGONOMETRY ITS EASY