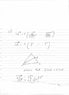Easy Vector Question | Picture Included | Homework Help

[Ed Aboud]

Homework Statement

Check the picture.

Homework Equations

The Attempt at a Solution

I'm sure it's very simple but I just can't seem to get it. I've been sitting here staring at the page for a while now with no joy. Check the picture for my attempt.
Thanks very much for any help, greatly appreciated.

 

[Ed Aboud]

Can anyone help with this?

 

[rock.freak667]

well you are correct in saying that \hat{b}=\frac{\vec{ab}}{|ab|} and that \hat{c}=\frac{\vec{ac}}{|ac|}.

and if \vec{ad} = t( \hat{b} - \hat{c}) what does that tell you about the direction of that vector?

How would you find the vector bc?

then how do you get the angle between two vector lines?

 

[Ed Aboud]

Ah I see it now so \vec{ad} = t ( \hat{cb} )
Therefore \vec{ad} is perpendicular to \hat{cb}
Therefore \vec{ad} is the perpendicular bisector of the the line bc.
Thank you very much for your help!