Trojan666ru
- 104
- 0
I was in a debate with a guy about "how does a spinning disk may look like in relativity."
His point was that the disk will be flat as always. But the radius will be curved, i couldn't actually imagine it.
He gave me a picture too
http://casa.colorado.edu/~ajsh/sr/cartbig_gif.html
So i come up with a model, but he rejects it saying the disk will be always flat
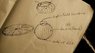
This is my explanation with picture
It's my drawing and you can see that when the disk spinns at relativistic velocity, the circumference shrinks but the radius has to be kept same
In this way the radius of the sphere can be kept same and
the circumference will be length contacted, thus the disk
becomes a hollow sphere
His point was that the disk will be flat as always. But the radius will be curved, i couldn't actually imagine it.
He gave me a picture too
http://casa.colorado.edu/~ajsh/sr/cartbig_gif.html
So i come up with a model, but he rejects it saying the disk will be always flat
This is my explanation with picture
It's my drawing and you can see that when the disk spinns at relativistic velocity, the circumference shrinks but the radius has to be kept same
In this way the radius of the sphere can be kept same and
the circumference will be length contacted, thus the disk
becomes a hollow sphere