Elastic Ball Problem: Is Something Wrong?

[IamVector]

Homework Statement

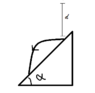
An elastic ball is released above an inclined plane
(inclination angle α) at distance d from the plane. What is
the distance between the first bouncing point and the second?
Collisions occur without friction.

Relevant Equations

the answer I got is 8dsinα but given answer is 8dtanα

anything wrong with sol or my answer?

 

[phinds]

Draw a diagram and show your work

 

[IamVector]

Draw a diagram and show your work

v² = √(2dg)
splitting into components
component ∥ to plane = v(sinα)
and as collosion is elastic component ⊥ plane = v(cosα)
thus time of flight = 2*t = 2* √(2d/g) = √(8d/g) = T
now s(distance) = (√(2dg) sinαT + ½ gsinαT²
thus by subsitution
s = 8dsinα

 

[IamVector]

Draw a diagram and show your work

??

 

[haruspex]

"at distance d from the plane"
Not clear whether it is the vertical distance or the shortest distance.

thus time of flight = 2*t = 2* √(2d/g)

After the first bounce? How do you get that? Remember, it will spend longer coming down than rising.

 

[IamVector]

"at distance d from the plane"
Not clear whether it is the vertical distance or the shortest distance.

After the first bounce? How do you get that? Remember, it will spend longer coming down than rising.

I am bad at making diagram on my computer hope it will help a bit .

 

[haruspex]

I am bad at making diagram on my computer hope it will help a bit .

Ok, but how do you get the range to the second bounce?

 

[IamVector]

Ok, but how do you get the range to the second bounce?

there was a component of gravity perpendicular to plane and one parallel to it so I used perpendicular one to find the time of flight and parallel one to find the range as shown in #3

 

[haruspex]

there was a component of gravity perpendicular to plane and one parallel to it so I used perpendicular one to find the time of flight and parallel one to find the range as shown in #3

Ok, very good.
I agree with your answer except, as I mentioned, it says d is the distance from the plane; it doesn’t say the height above the plane. But that would make the answer even larger, so doesn’t help.

 

[IamVector]

Ok, very good.
I agree with your answer except, as I mentioned, it says d is the distance from the plane; it doesn’t say the height above the plane. But that would make the answer even larger, so doesn’t help.

what does "from the plane means??" ball is released above the inclined plane so won't it be the height above it? or are the terms "inclined plane" and "plane a bit different" like inclined or horizontal?

 

[haruspex]

what does "from the plane means??

The distance from a point to a plane is generally taken to be along the shortest path, i.e. normal to the plane.

 

[Orodruin]

Ok, very good.
I agree with your answer except, as I mentioned, it says d is the distance from the plane; it doesn’t say the height above the plane. But that would make the answer even larger, so doesn’t help.

Yes it does, tan is larger than sin by a factor 1/cos, which just happens to be the same factor by which the vertical distance is larger than the shortest distance.

 

[haruspex]

Yes it does, tan is larger than sin by a factor 1/cos, which just happens to be the same factor by which the vertical distance is larger than the shortest distance.

Doh! I misremembered which way round the book answer and the OP's answer were.
Thanks.

 

[IamVector]

Yes it does, tan is larger than sin by a factor 1/cos, which just happens to be the same factor by which the vertical distance is larger than the shortest distance.

ohk so we were asked to find horizontal displacement.

 

[Orodruin]

ohk so we were asked to find horizontal displacement.

No. That would be shorter than the displacement along the slope.

The issue is exactly what @haruspex has been zooming in on - you are told the distance to the plane, not the height above the plane.

 

[IamVector]

No. That would be shorter than the displacement along the slope.

The issue is exactly what @haruspex has been zooming in on - you are told the distance to the plane, not the height above the plane.

does it means perpendicular distance like this??

 

[Orodruin]

does it means perpendicular distance like this??View attachment 258622

Yes, that is typically what you mean when you say "distance to the plane", i.e., the shortest possible distance to a point on the plane.

 

[IamVector]

Yes, that is typically what you mean when you say "distance to the plane", i.e., the shortest possible distance to a point on the plane.

ohk
that is why its tan except sin, I completely misunderstood it thanks for help : ) .