- #1
stunner5000pt
- 1,461
- 2
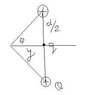
Two postitive charges +Q are held at fixed distance d from each other. A particle of charge -q is placed at the mid point between them and given a small displacement y, on the line perpendicular to the line joining them and released. Show that hte particle described SHM of period [tex] (\frac{\epsilon_{0} m \pi^3 d^3}{qQ})^\frac{1}{2} [/tex]
i drew a figure of what this might look like.
I was wondering if i had to prove that this particle is going to undergo SHM. I can easily say that at points +y and -y the force on the particle is the maximum and is [tex] \pm \frac{Qqd}{4 \pi \epsilon_{0} tan^2 \theta} [/tex]
would i then simply plug the acceleration of this force into th4e SHM equation??
But how would i get rid of the tan theta?? I doesn't appear in the answer they want.. after all.
i drew a figure of what this might look like.
I was wondering if i had to prove that this particle is going to undergo SHM. I can easily say that at points +y and -y the force on the particle is the maximum and is [tex] \pm \frac{Qqd}{4 \pi \epsilon_{0} tan^2 \theta} [/tex]
would i then simply plug the acceleration of this force into th4e SHM equation??
But how would i get rid of the tan theta?? I doesn't appear in the answer they want.. after all.