physics604
- 92
- 2
1. What current flows through the 11.0 Ω resistor?
a) 0.21 A
b) 0.27 A
c) 0.93 A
d) 1.2 A
To summarize:
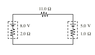
V1 = 8.0 V
V2 = 5.0 V
R1 = 2.0 Ω
R2 = 11.0 Ω
R2 = 1.0 Ω
I know we shouldn't attach pictures, but the diagram does make the question a lot easier to understand.
V=IR
VT = ε-Ir
RT = 11.0 + 2.0 + 1.0 = 14.0 Ω
VT = 8.0 + 5.0 = 13.0 V
IT = V/R = 13.0/14.0 = 0.93 A.
And since current should be the same throughout a series circuit, the current through the 11.0 Ω resistor should be 0.93 too. My answer is wrong though.
Correct answer: a) 0.21 A, but I don't understand why. Please help me?
a) 0.21 A
b) 0.27 A
c) 0.93 A
d) 1.2 A
To summarize:
V1 = 8.0 V
V2 = 5.0 V
R1 = 2.0 Ω
R2 = 11.0 Ω
R2 = 1.0 Ω
I know we shouldn't attach pictures, but the diagram does make the question a lot easier to understand.
Homework Equations
V=IR
VT = ε-Ir
The Attempt at a Solution
RT = 11.0 + 2.0 + 1.0 = 14.0 Ω
VT = 8.0 + 5.0 = 13.0 V
IT = V/R = 13.0/14.0 = 0.93 A.
And since current should be the same throughout a series circuit, the current through the 11.0 Ω resistor should be 0.93 too. My answer is wrong though.
Correct answer: a) 0.21 A, but I don't understand why. Please help me?
Attachments
Last edited: