Electric field and potential at the center of a square of four point charges

[Clara Chung]

Homework Statement

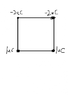
Four point charges are placed at the corners of a square of side 1m as shown in Fig 18.54 Find
a) the electric field, and
b) the electric potential at the center of the square

Photo is attached

Homework Equations

coulomb's law
Ans of a=76.3 x 10^3 NC^-1 upward
Ans of b=-25.4x 10^3 V

The Attempt at a Solution

I can do part a by 2x(2/10^6)x2x8.99x10^9xsin45 + 2x(2/10^6)x8.99x10^9xsin45=76.3 x 10^3 NC^-1 upward.
I just attempted b part by 2x(2/10^6)xroot2x8.99x10^9xsin45 + 2x(1/10^6)xroot2x8.99x10^9xsin45
because V=ED I just multiply each term by its length 1/root2 from the center.
But the answer seems to be one third of the answer from part a, please teach me how to do.

 

[Simon Bridge]

Try doing it from the definition of the electric potential.

 

[Clara Chung]

Use the definition: work done per charge from infinity to the center?

 

[cnh1995]

Use the definition: work done per charge from infinity to the center?

That will work. Potential at a point at a distance r due to a charge q is kq/r. You can add and subtract potentials aglebraically.

 

[Clara Chung]

Thanks I forget that voltage is scalar

 

[Simon Bridge]

Well done.