Broem
- 9
- 0
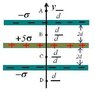
Homework Statement
What is the electric field at point A in the unit of σ/ε0?
Homework Equations
E=σ/2ε
The Attempt at a Solution
I just want to make sure my thinking behind this is correct.
From the center we have +5σ. To find the A what I did is subtract the other two -σ from the 5: this gives me 5-1-1 = 3.
From here I just plug in: 3σ/2ε which in the units = 1.5 σ/ε
Is this the correct approach?