Electric field in the center of uniformly polarized cylinder

[gruba]

Homework Statement

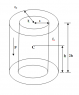
Hollow dielectric cylinder, with inner radius a, outer radius b, and height 2h is uniformly polarized by volume. Polarization vector is normal on the bases of a cylinder. Intensity of polarization vector is given, P. The surrounding area is vacuum. Calculate intensity of electric field in center of the cylinder (at point C)

Homework Equations

-Cylindrical geometry
-Polarization vector

The Attempt at a Solution

If approximated, intensity of electric field could be E= -P/ε₀ (field between two oppositely charged planes). But, we don't know the exact values for dimensions of a cylinder. Could someone give a hint on this, I am stuck here for a while.

The result should be E= -Ph( 1/(√a²+h²)-1/(√b²+h²)) / ε₀

Thanks for replies.

 

[TSny]

Certain parts of the surface of the cylinder will have an effective surface charge density due to the polarization.