Electric field of a ring and beads

[wbetting]

Homework Statement

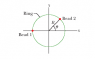
a plastic ring of radius R = 50.4 cm. Two small charged beads are on the ring: Bead 1 of charge +2.00 μC is fixed in place at the left side; bead 2 of charge +6.00 μC can be moved along the ring. The two beads produce a net electric field of magnitude E at the center of the ring. At what (a) positive and (b) negative value of angle θ should bead 2 be positioned such that E = 2.22 × 105 N/C?

Homework Equations

Enety by -q2sinθ/4πε0R^2
Enetx by q1/4πε0R^2 - q2cosθ/4πε0R^2

The Attempt at a Solution

so i found enet of y and x by equations above then did E^2=(q1^2+q1^2-2q1q2cosθ/(4πε0R^2)^2

which simples to

θ=inverse cos [(q1^2+q1^2- (4πε0R^2)^2E^2)/(2q1q2)]



basically when i take the cos its a neg number and you can't take cos of neg number so i am confused what i am doing wrong bc my professor said method was correct

 

[TSny]

The Attempt at a Solution

so i found enet of y and x by equations above then did E^2=(q1^2+q1^2-2q1q2cosθ/(4πε0R^2)^2

which simples to

θ=inverse cos [(q1^2+q1^2- (4πε0R^2)^2E^2)/(2q1q2)]
basically when i take the cos its a neg number and you can't take cos of neg number so i am confused what i am doing wrong bc my professor said method was correct

You can take the cosine of a negative number (e.g., cos(-30^o) = .5) and you can also take the inverse cosine of a negative answer (e.g., inv cos (-.5) = 120^o).

But, anyway, if I substitute the numbers into your expression for θ, I find that you should be taking the inverse cosine of a positive number and you get a positive angle for θ.

Overall, your work looks good to me.