I think I have managed to explain to myself what has been said here so far to my satisfaction. I present it below to summarize my ideas for anyone who might be interested.
Start with ##d\vec E=\dfrac{k dq(\vec r-\vec r')}{|\vec r-\vec r')|^3}##. Consider an element on the sphere at ##\theta## and ##\phi##. The point of observation is on the ##z##-axis. Then
##\vec r = z~\hat z##
##\vec r' = R \sin\theta \cos\phi~\hat x+R \sin\theta \sin\phi~\hat y+ R \cos\theta ~\hat z##
##dq=\sigma R^2\sin\theta~ d\theta d\phi##
##(\vec r-\vec r')=(-R \sin\theta \cos\phi~\hat x-R \sin\theta \sin\phi~\hat y+(z- R \cos\theta) ~\hat z)##
##|\vec r-\vec r'|=(R^2+z^2-2zR\cos\theta)^{1/2}##
##d\vec E=\dfrac{k \sigma R^2\sin\theta (-R \sin\theta \cos\phi~\hat x-R \sin\theta \sin\phi~\hat y+(z- R \cos\theta) ~\hat z)}{(R^2+z^2-2zR\cos\theta)^{3/2}}d\theta~ d\phi##
Integration over ##\phi## results in an axial contribution only,
##dE_z=\dfrac{2 \pi k \sigma R^2\sin\theta (z- R \cos\theta)}{(R^2+z^2-2zR\cos\theta)^{3/2}}d\theta.##
The theta integral is done using the standard substitution ##\int_0^{\pi}f(\cos\theta)\sin\theta~d \theta \rightarrow \int_{-1}^{+1}f(u)~du.## Then
$$E_z=2 \pi k \sigma R^2\int_{-1}^{+1}\frac{(z- R u)}{(R^2+z^2-2zRu)^{3/2}}du.$$The integral can be easily done by a second substitution, ##y=R^2+z^2-2zRu##.$$\begin{align}\int_{-1}^{+1}\frac{(z- R u)}{(R^2+z^2-2zRu)^{3/2}}du & =\left. \frac{u z-R}{z^2 \sqrt{R^2-2 R u z+z^2}}\right |_{-1}^{+1} \nonumber \\ &=\frac{z-R}{z^2 \sqrt{R^2-2 R z+z^2}}-\frac{-R-z}{z^2 \sqrt{R^2+2 R z+z^2}}\nonumber \\ & =\frac{z-R}{z^2 \sqrt{(R-z)^2}}+\frac{R+z}{z^2 \sqrt{(R+z)^2}}.\nonumber\end{align}$$ Thus, $$\begin{align}E_z=\frac{2 \pi k \sigma R^2}{z^2}\left[\frac{z-R}{ \sqrt{(R-z)^2}}+\frac{R+z}{ \sqrt{(R+z)^2}}\right]=\frac{2 \pi k \sigma R^2}{z^2}\left[\frac{z-R}{ \sqrt{(R-z)^2}}+1\right]\end{align}$$ We distinguish three cases.
Case I: ##R >z##, inside the shell.
Then ##\sqrt{(R-z)^2}=R-z## in which case $$E_z=\frac{2 \pi k \sigma R^2}{z^2}\left[\frac{z-R}{ R-z}+1\right]=\frac{2 \pi k \sigma R^2}{z^2}\left[-\frac{R-z}{ R-z}+1\right]=0$$ as expected.
Case II: ##z >R##, outside the shell.
Then ##\sqrt{(R-z)^2}=z-R## in which case $$E_z=\frac{2 \pi k \sigma R^2}{z^2}\left[\frac{z-R}{ z-R}+1\right]=\frac{4 \pi k \sigma R^2}{z^2}=\frac{\sigma R^2}{\epsilon_0 z^2}.$$When we set ##z=R##, ##E_z=\dfrac{\sigma}{\epsilon_0}.##
Case III: ##z =R##, on the shell.
Then $$E_z=\frac{2 \pi k \sigma R^2}{R^2}\left[\frac{R-R}{ \sqrt{(R-R)^2}}+1\right]=2 \pi k \sigma\left[\frac{0}{ \sqrt{(0)^2}}+1\right]=\text{undefined}$$
The article by F.M.S. Lima (reference in post #26) sets ##z=R## before doing the integral. In that case, $$\int_{-1}^{+1}\frac{(z- R u)}{(R^2+z^2-2zRu)^{3/2}}du~\rightarrow~\int_{-1}^{+1}\frac{(R-Ru)}{(R^2+R^2-2R^2u)^{3/2}}du=\frac{1}{2^{3/2}R^2}\int_{-1}^{+1}\frac{(1-u)}{(1-u)^{3/2}}du.$$This last integral is problematic if we allow the upper limit, corresponding to ##\cos0##, be equal to 1. This is where the "hole" comes in. We set the upper limit equal to ##1-\epsilon~~(\epsilon > 0)## and proceed. $$\frac{1}{2^{3/2}R^2}\int_{-1}^{1-\epsilon}\frac{(1-u)}{(1-u)^{3/2}}du=\frac{1}{2^{3/2}R^2}\int_{-1}^{1-\epsilon}\frac{du}{(1-u)^{1/2}}=\left .-\frac{2\sqrt{1-u)}}{2^{3/2}R^2}\right |_{-1}^{1-\epsilon}=\frac{1}{R^2}\left(1-\sqrt{\frac{\epsilon}{2}}\right).$$We multiply by the constant and close the "hole" by setting ##\epsilon=0## to get the electric field at ##R##, $$E_z=2 \pi k \sigma R^2 \frac{1}{R^2}\left(1-\sqrt{\frac{\epsilon}{2}}\right)= \frac{ \sigma}{2\epsilon_0}.$$Notably, Equation (1) gives the electric field everywhere. If we strip the constants and consider a unit sphere, the functional dependence on ##z## can be rewritten as $$f(z)=\frac{1}{2z^2}(\text{Sgn}[z-1]+1)$$ producing the plot shown below.
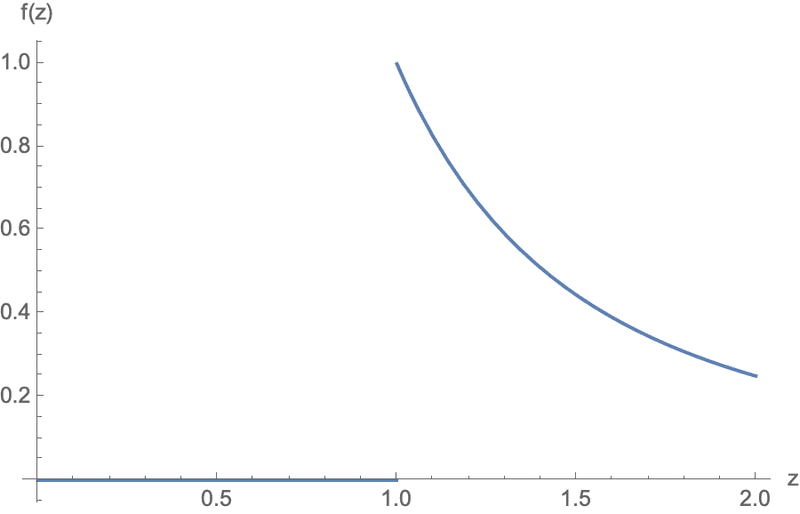
We also note that without the ##z^{-2}## dependence we have a shifted
Heaviside step function, ##h(z)=\frac{1}{2}(\text{Sgn}[z-1]+1)## that is equal to zero for ##z<1## and equal to 1 for ##z>1.## Thus, the value of ##\frac{1}{2}## that multiplies the value ##\frac{\sigma}{\epsilon_0}## of the field arbitrarily close to the outer surface of the shell is the Heaviside half-maximum.
I have explained this to myself in a non-mathematical way as follows: Let's say that, for some reason e.g. quantum effects or discreteness of charges, the transition of the electric field from zero (just inside) to ##\frac{\sigma}{\epsilon_0}## (just outside) is not infinitely sharp. Then it can be approximated by some function, that goes smoothly from zero to ##\frac{\sigma}{\epsilon_0}##. It is reasonable to say that, by symmetry, the point that is neither inside nor outside the "surface" is the inflection point of the smoothing function, i.e. the Heaviside half-maximum (see Wikipedia article).