Electric flux through a surface

[Plasmosis1]

Homework Statement

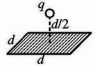
A point charge q is situated a distance d/2 above a square surface of side d as shown (see attached).
a) It cannot be determined
b) 2q/ε₀d
c) q/4\piε₀
d) q/\piε₀d²
e) q/6ε₀

Homework Equations

\Phi=q_enc/ε₀=\ointE*dA

The Attempt at a Solution

Shouldn't the answer be zero because whatever enters the area also leave the area? If not I know I should use the integral of E*dA but I don't know what E would be.

 

[rude man]

If the area were a thin volume you'd be correct, the net flux into the volume = 0, but flux thru a surface A = the integral over the surface of the dot-product of the electric field E and an element of surface area dA: flux = ∫∫ E*dA.


So yes, you need to integrate E*dA over the surface. dA is normal to the surface at every point on the surface.

 

[nasu]

You can manage without integration.
Imagine the charge is in the middle of a cube with side d.
Due to symmetry, the flux through each face of the cube is the same.
And the total flux through the cubic, closed surface can be found from Gauss' law.

 

[rude man]

Nasu has come up with the right and simple way to solve this.