Swagger
- 19
- 0
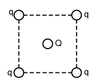
Find the charge Q that should be placed at the centre of the square of side 7.70E+0 cm, at the corners of which four identical charges +q = 11 C are placed so that the whole system is in equilibrium.
(picture attached)
I know that the sum of all the forces must equal zero. I also figured out that the force on the small q's is 1.834E14. Where do I go from here?
(picture attached)
I know that the sum of all the forces must equal zero. I also figured out that the force on the small q's is 1.834E14. Where do I go from here?