Electrodynamics: Amplitude of currents

[Niles]

Homework Statement

Hi all.

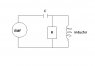
Please take a look at the attached circuit. I've have found the amplitude of the current through the resistance to be:

<br /> \left| {I_0 } \right| = \frac{{\varepsilon _0 }}{{\left| {R - \frac{R}{{\omega ^2 LC}} + \frac{i}{{\omega C}}} \right|}},<br />

where ε_0 is the amplitude of the EMF, and the EMF is given by ε_0 cos(ωt). This is all good (and correct too! ), but in my book it says that in general, the amplitude of the current is given by:

<br /> \left| {I_0 } \right| = \frac{{\varepsilon _0 }}{{\left| Z \right|}},<br />

where Z is the impedance. So according to my book, the amplitude of the current through the resistance must be:

<br /> \left| {I_0 } \right| = \frac{{\varepsilon _0 }}{{\left| {R - i\omega L + \frac{i}{{\omega C}}} \right|}}.<br />

What's wrong here? I mean, I know my result is correct, but it is obviously not the same as the one my book wants. What impedance is it I have in my denominator then?

Thanks in advance.Niles.

 

[marcusl]

Something's amiss here. Don't know where your first equation came from, but the third equation (from your book, you say) describes a series tank circuit and not the series/parallel circuit you drew.

 

[Redbelly98]

Note that

{R - i\omega L + \frac{i}{{\omega C}}}

would be the impedance if all three elements were in series. However that is not the case in the circuit you show.