othonmp
- 5
- 0
Homework Statement
What is the compensative system of this combination of resistors?
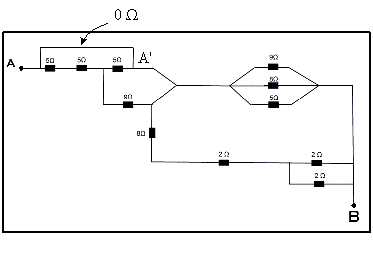
http://img545.imageshack.us/img545/6610/circuitoi.jpg
Last edited by a moderator:
othonmp said:Homework Statement
What is the compensative system of this combination of resistors?
http://img545.imageshack.us/img545/6610/circuitoi.jpg
dinospamoni said:I'm not sure what you're referring to. Do you mean the total resistance?
othonmp said:Yes,I mean the total resistance =]
sorry, English is not my first language
gneill said:Okay. What techniques have you learned about for reducing (simplifying) resistor networks? Can you spot any opportunities to apply them in the given circuit?
othonmp said:I know about combinations in parallel and in series, I could spot the parallel combination on the superior right corner (9Ω,8Ω,5Ω), they can be reduced to a resistance of aproximately 2.29Ω
there is a combination in series(8Ω,2Ω) that is equal a resistance of 10Ω
as well, there is a combination in parallel near B(2Ω,2Ω) that is equal 1Ω
but it just this, I don't know what I have to do with the first part, where there's are 5Ω resistances and a 9Ω resistance
gneill said:Yes, you should replace those parallel and serial resistances with their reduced values as you've stated, and continue to combine any more such opportunities that arise from those reductions.
Regarding the grouping in the top left corner near A, note the wire that bridges the combination. Since it's a perfect conductor, its resistance is zero. That ties together the points A and A'. What then must be the resistance between A and A'?
gneill said:Yes, that's the right procedure