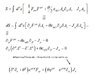Electrodynamics in two space dimensions :-(

Click For Summary
SUMMARY

The forum discussion centers on solving a problem in electrodynamics within two space dimensions. The user, TED, seeks assistance with their equations of motion (EOM) derivation, which contains errors in indices and possibly sign or coefficient inaccuracies. A suggestion is made to redo the derivation in detail and to calculate the expression (θ η^{μν} - ε^{μνα} ∂_α) J_ν using the corrected EOM. This approach is expected to yield the left side of the equation accurately.

PREREQUISITES
  • Understanding of electrodynamics principles in two dimensions
  • Familiarity with equations of motion (EOM) in physics
  • Knowledge of tensor notation and manipulation
  • Experience with mathematical derivations in theoretical physics
NEXT STEPS
  • Review the derivation of equations of motion in electrodynamics
  • Study tensor calculus and its application in physics
  • Learn about the significance of indices in tensor equations
  • Explore the role of coefficients and signs in physical equations
USEFUL FOR

Students and researchers in theoretical physics, particularly those focusing on electrodynamics and mathematical physics, will benefit from this discussion.

ted1986
Messages
22
Reaction score
0
Hi all,

I've got this problem (which is attached as q1.jpg).

I've tried to solve it, but I'm stuck... my solution is also attached (my_sol1.jpg).

PLS help me :-(

Thnx

TED
 

Attachments

  • q1.jpg
    q1.jpg
    37.2 KB · Views: 532
  • my_sol1.jpg
    my_sol1.jpg
    24.3 KB · Views: 525
Physics news on Phys.org
In your derivation of the EOM, you got some indices wrong and forgot an A^μ. Maybe there are also sign or coefficient errors, haven't checked it in detail. I propose you to redo it in more detail.
For the next step, derive your EOM once and calculate ( θ η^{μν} - ε^{μνα} ∂_α ) J_ν using your EOM and the derived version, which should give you the left side.
 
Thanks! I'll try it...

Do I know you from somewhere ? ;-)
 
Don't know if I have seen you, but if you were born in 1986, that's possible ... you have a private message.
 

Similar threads

Equilibrium arrangement angle of 4 charges in a square
  • · Replies 2 ·
Replies
2
Views
2K
Help with Time-Independent Perturbation Theory "Good" States Proof
  • · Replies 4 ·
Replies
4
Views
953
Need help with calculating a Cv in PHYWE's Heat Capacity of gases
  • · Replies 4 ·
Replies
4
Views
2K
Technical drawing: reference dimensions
  • · Replies 12 ·
Replies
12
Views
4K
Undergrad How Does the Flow Equation Apply in Higher Dimensional Phase Spaces?
  • · Replies 7 ·
Replies
7
Views
1K
How Does Equation 4.39 Apply to Dipole Moments in Griffith's Problem 4.37?
  • · Replies 4 ·
Replies
4
Views
3K
Why Is the d-Orbital Considered in Sc Term Symbols?
  • · Replies 5 ·
Replies
5
Views
3K
Find the Period of Oscillation for a Mass Falling Through a Tunnel Through the Earth
  • · Replies 7 ·
Replies
7
Views
1K
Classical What Are the Best Resources for Learning Electrodynamics?
  • · Replies 21 ·
Replies
21
Views
5K
Phase space of a harmonic oscillator and a pendulum
  • · Replies 5 ·
Replies
5
Views
2K