Electrodynamics problem (circuit with two sources)

[Rugile]

Homework Statement

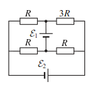
In the circuit (see attachment) we have 2 sources. If we decrease the EMF of the first source (ε₁) by 1.5V, the current changes in every branch of the circuit. How does the EMF of the source ε₂ has to be changed, so that the current through the ε₁ source would be the same as previously?

Homework Equations

Kirchhoff's laws

The Attempt at a Solution

I guess what we need to do here is to find the dependency of ε₁ on ε₂. Is using the Kirchhoff's equations the best way here? I wrote down such eq:
<br /> I_3R + I_1r_1 + I_5R = \epsilon_1<br />
<br /> 3I_4R + I_6R + I_1r_1 = \epsilon_1<br />
<br /> I_2r_2 + I_6R - I_5R = \epsilon_2<br />
<br /> I_3 + I_4 = I_1<br />
<br /> I_5+I_6 = I_1<br />
<br /> I_3 = I_5 + I_2<br />
<br /> I_4 + I_2 = I_6<br />
Here r₁, r₂ - internal resistances of the sources (since there is current flowing through the sources, they must have internal resistances, right?)
I₃ - top left resistor
I₅ - down left resistor
I₄ - top right resistor
I₆ - down right resistor
I₁ - ε₁ current
I₂ - ε₂ current
But couldn't solve the system :/
Maybe there is a better way to do this? It seems to me there should be something simpler than system of 8 equations?
Any help appreciated!

 

[dauto]

Assume that r₁ and r₂ are negligible compared to R unless otherwise stated and can be removed from the equations.

 

[Rugile]

Assume that r₁ and r₂ are negligible compared to R unless otherwise stated and can be removed from the equations.

But then I₁ and I₂ are removed, too, and (I made a mistake in the first post here) it is not possible to find the dependency of I₁ on the other parameters (like ε₁, ε₂)? Or am I wrong and we are looking for something else?

 

[dauto]

No, I₁ and I₂ are not removed. They show up in the junction equations.

 

[Rugile]

Yes, thanks a lot, that was it!