jhonnyS
- 2
- 0
- TL;DR Summary
- the electron wave function for a determined energy level, without superposition of states, decreases its frequency as the distance from the center increases. So the "oscilation" shouldn't be slower with distance from the center?
As we see in this Phet simulator, this is only the real part of the wave function, the frequency decreases with the potential, so lose energy as moves away the center.
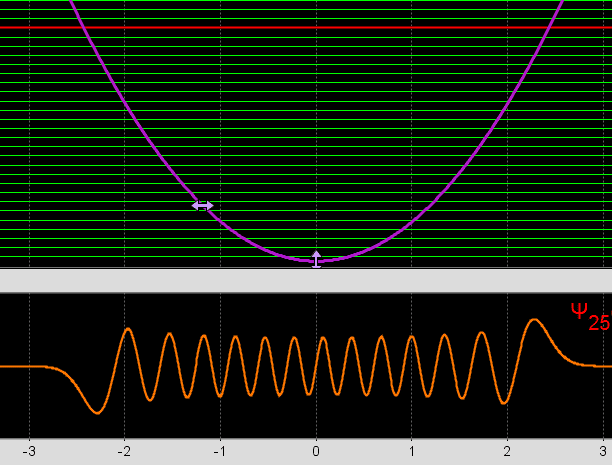
we se this real-imaginary animation in Wikipedia, wave C,D,E,F. Because with less energy, the frequency of quantum wave decreases, and the speed decreases too, the oscillation wouldn't be slower acording to frequency variation in image F for example? (the same way we see image D oscillating slower than F)
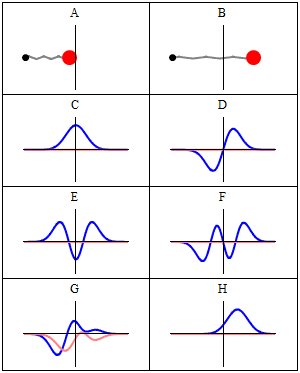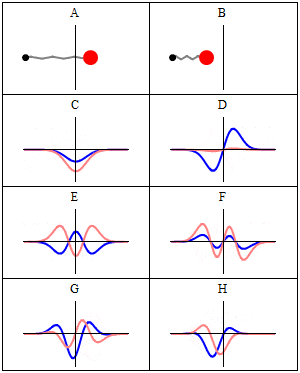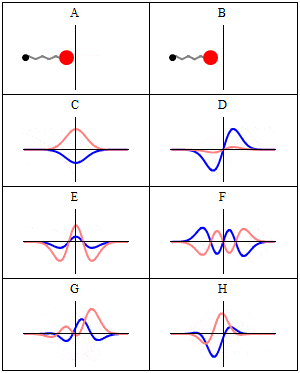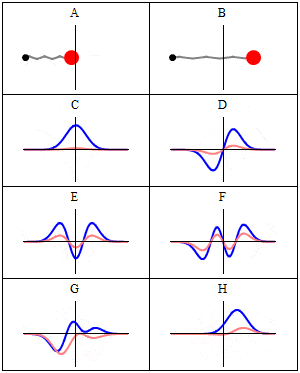
The desired response, without formulas, and without Schrödinger time independent ecuation, just explained
https://en.wikipedia.org/wiki/Quantum_harmonic_oscillator
thank you!
we se this real-imaginary animation in Wikipedia, wave C,D,E,F. Because with less energy, the frequency of quantum wave decreases, and the speed decreases too, the oscillation wouldn't be slower acording to frequency variation in image F for example? (the same way we see image D oscillating slower than F)
The desired response, without formulas, and without Schrödinger time independent ecuation, just explained
https://en.wikipedia.org/wiki/Quantum_harmonic_oscillator
thank you!
 ##\quad## !
##\quad## !