Electrostatic force electroscope

[joanne]

electroscope

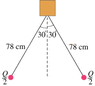
A large electroscope is made with “leaves” that are 78-cm-long wires with tiny 24-g spheres at the ends. When charged, nearly all the charge resides on the spheres. If the wires each make a 3.0E1° angle with the vertical (see figure), what total charge Q must have been applied to the electroscope? Ignore the mass of the wires.

*here is what I did...and got stuck in the middle of doing this problem*

Well, first I found the distance between Q/2 and Q/2. Then I applied this equation http://i5.photobucket.com/albums/y178/besuu4/b836e8b8cc7c00400c5910d3eca76e37.png to find Q. The problem is I don't have F (force) value to solved it by using the equation I provided. Anyway...I am just confusing myself. Hints are welcome. Thanks.

 

[LeonhardEuler]

You know that the charges are not moving. This means they must be in equillibrium. Set up a free body diagram.

 

[Chi Meson]

You are told to ignore the mass of the wires. But don't ignore the mass of the charges.

Assume this occurs on Earth. (Weight a minute, is this a clue to the "missing force"?)

Can you say "trigonometry"?

 

[joanne]

I think I get your clue, Chi Meson.

I know this is oscesles (sp?) triangle so the other two angle must be equal which is 60 degrees. I then used Sin(30)=X/78=39 to find the length and mutliple by 2 to get the full length (happened to be 78cm).

Then I used F=ma to find the force. F=(.024kg)(9.8m/s^2)=.2352N.
after that, I used this equation http://i5.photobucket.com/albums/y178/besuu4/b836e8b8cc7c00400c5910d3eca76e37.png to solve for Q.

.2352N=1/4*pi*8.85e-12*(Q^2/78cm^2)
So the answer is Q=1.59e-7 C, correct?

 

[joanne]

so...right or not? Thanks.

 

[HiPPiE]

Not quite! The forces don't have to be equal for equilibrium as they're not in opposite directions. Also, the charge on each ball isn't Q. Inquire further for more help.

 

[Doc Al]

joanne,

Start by identifying all the forces acting on one of the spheres. (I count three forces acting.) Label the forces in a diagram, then apply the conditions for static equilibrium: The net force must be zero. (Hint: Write two equations. One for vertical components; one for horizontal components.)

 

[HiPPiE]

Well not quite for vertical and horizontal... right? But yeah for two perpendicular directions. See if you can find out which :)
Edit: well I guess it doesn't matter, but one way you can ignore 1 of the 3 forces.