Why Is Work Positive When Done Against the Electric Field?

[lys04]

Homework Statement

Several questions relating to work, electric potential energy, and potential difference.

Relevant Equations

kq1q2/r
kq/r

I have several questions relating to electrostatics:
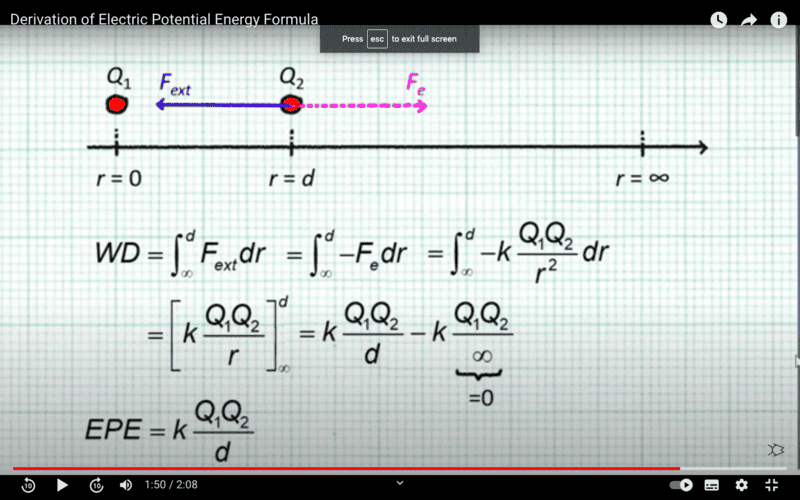
first of all, in this derivation for the formula of the electric potential energy:
work is being done against the electric field right, so the work should be negative, but in this case it's positive. I'm wondering if it's because the direction of dr and the force should be in the same direction so when you take the dot product it's a positive result? Then the work done will be negative and according to the equation W=-delta U then U will be equal to positive kq1q2/r?

Second question, the equation V=kq/r can only be used on point charges right since it comes from V=U/q and the equation for U comes from work which involves Coulomb's law, which only applies for point charges.
Third question, why is the potential difference for a spherical conductor at the surface kq/r? This relates to my question above, how can the spherical conductor be assumed to be a point charge at the surface?
Last question, why is the potential difference inside the spherical conductor not 0 if there is no electric field? Also, I saw some posts saying that the potential difference inside is equal to that on the surface because there is no electric field inside and so there is no work done, so the difference in potential is 0 and hence Vinside=Vsurface. But the surface isn't INSIDE the sphere anymore? Or am I just overthinking it?

 

[haruspex]

work is being done against the electric field right, so the work should be negative

No, if work is done in opposing the field then the work done is positive. Think about lifting a weight.

V=kq/r can only be used on point charges

It also turns out to apply outside uniform spherical shells, r being the distance from the centre of the sphere.

how can the spherical conductor be assumed to be a point charge at the surface?

It is not an assumption, and it is not like a point charge "at the surface".
It is a provable result that if a spherical shell radius r has a uniformly distributed charge Q at its surface then the potential at a point distance d from the centre of the sphere is:

• kQ/d if d>r
• kQ/r if d<r

the surface isn't INSIDE the sphere

Ignore the material of the sphere and just consider the infinitesimal layer of charge. Since there is no internal field, the inside must have the same potential as the surface.

 

[Steve4Physics]

It's often better to ask only one question at a time. Or answers /conversations about different questions get muddled-up with each other. However...

first of all, in this derivation for the formula of the electric potential energy:
work is being done against the electric field right, so the work should be negative, but in this case it's positive. I'm wondering if it's because the direction of dr and the force should be in the same direction so when you take the dot product it's a positive result? Then the work done will be negative and according to the equation W=-delta U then U will be equal to positive kq1q2/r?
View attachment 330434

Consider the case where $Q_1$ and $Q_2$ are both positive. A leftwards external force ($\vec F_{ext}$) is applied to $Q_2$, moving it leftwards towards $Q_1$. $\vec F_{ext}$ and its displacement are in the same direction (both to the left, both negative) and their dot product is therefore positive. The work done by $\vec F_{ext}$ is positive.

Energy has been supplied by $\vec F_{ext}$ and this has increased the system’s potential energy,

(Note that the work done done by the electric force, $\vec F_E$, is negative. This work is minus the charge in potential energy. This is may be easiest to understand by considering gravity. If you drop a stone, gravity does positive work (providing kinetic energy); as a consequence, the change in gravitational potential energy is negative.)

Second question, the equation V=kq/r can only be used on point charges right since it comes from V=U/q and the equation for U comes from work which involves Coulomb's law, which only applies for point charges.

That's not a question . And it's not accurate. If you have a spherically symmetric charge distribution (e.g. a uniformly charged sphere), then outside the distribution, the field is identical to that produced by point charge of the same magnitude positioned at the centre of the distribution.

Third question, why is the potential difference for a spherical conductor at the surface kq/r? This relates to my question above, how can the spherical conductor be assumed to be a point charge at the surface?

See above.

Last question, why is the potential difference inside the spherical conductor not 0 if there is no electric field? Also, I saw some posts saying that the potential difference inside is equal to that on the surface because there is no electric field inside and so there is no work done, so the difference in potential is 0 and hence Vinside=Vsurface. But the surface isn't INSIDE the sphere anymore? Or am I just overthinking it?

If the potential is constant (though not necessarily zero) the electric field is zero. Can you see how that answers your question?

 

[kuruman]

first of all, in this derivation for the formula of the electric potential energy:
work is being done against the electric field right, so the work should be negative, but in this case it's positive. I'm wondering if it's because the direction of dr and the force should be in the same direction so when you take the dot product it's a positive result? Then the work done will be negative and according to the equation W=-delta U then U will be equal to positive kq1q2/r?

This is my answer to your "First of all question" which is a recurring issue when on applies the definition of work $dW=F~dr~\cos\!\theta$ and then tries to do an integral with lower and upper limits. The remedy is to ignore the relative direction between force and displacement and the sign of the charge and do it formally using the definition of work done by a force as a line integral. For this example,
1. Start with $~W_{AB}=\int_A^B \vec F \cdot d\vec r.$

2. Use unit vector notation to express the vectors
$~\vec E=\dfrac{kQ_1}{r^2}\mathbf{\hat r}~;~~\vec F=Q_2\vec E=\dfrac{kQ_1Q_2}{r^2}\mathbf{\hat r}.$
$d\vec{r}=dr~\mathbf{\hat r}.$

3. Find an expression for the integrand
$\vec F \cdot d\vec r=\left(\dfrac{kQ_1Q_2}{r^2}\mathbf{\hat r}\right)\cdot(dr~\mathbf{\hat r})=\dfrac{kQ_1Q_2}{r^2}dr.$

4. Integrate $$W_{AB}=kQ_1Q_2\int_{r_{\!A}}^{r_{\!B}} \frac{dr}{r^2}=-kQ_1Q_2\left(\frac{1}{r_{\!B}}-\frac{1}{r_{\!A}}\right)

.$$Note that with this formal method all negative signs are taken care of automatically and you don't have to worry about the relative orientation of vectors.

• If either one of the charges is negative, the work changes sign.
• If, instead of going from $r_{\!A}=d$ to $r_{\!B}=\infty$, you reverse path and go from $r_{\!B}=\infty$ to $r_{\!A}=d$, the work changes sign. The element $d\vec{r}$ is always and by definition equal to $~(+dr~\mathbf{\hat r}).$
• Double changes of sign, e.g. reverse the path and change the sign of one charge, do not change the sign of the work.

In short, let the unit vectors do the work for you (the pun is intentional.)

 

[lys04]

No, if work is done in opposing the field then the work done is positive. Think about lifting a weight.

It also turns out to apply outside uniform spherical shells, r being the distance from the centre of the sphere.

It is not an assumption, and it is not like a point charge "at the surface".
It is a provable result that if a spherical shell radius r has a uniformly distributed charge Q at its surface then the potential at a point distance d from the centre of the sphere is:

• kQ/d if d>r
• kQ/r if d<r

Ignore the material of the sphere and just consider the infinitesimal layer of charge. Since there is no internal field, the inside must have the same potential as the surface.

Oh really, the slides my professor gave me said doing work against the field is negative..

 

[haruspex]

Oh really, the slides my professor gave me said doing work against the field is negative..

That slide is quite misleading. It doesn't specify which work is being considered as positive or negative, the work done by the field or the work done by the external force.

Better would be:

• If a charge is moving in the direction it would naturally move, the E field is doing positive work
• If a charge is moving opposite to the direction it would naturally move, the E field is doing negative work

There might or might not be an external force. If the speed is constant there must be one and we can add:

• If a charge is moving in the direction it would naturally move, the external force is doing negative work
• If a charge is moving opposite to the direction it would naturally move, the external force is doing positive work

Or if no other force is present then the speed must be changing and the charge must have mass:

• If a charged mass is moving in the direction it would naturally move, with no other forces present, the E field is doing positive work accelerating the mass
• If a charged mass is moving opposite to the direction it would naturally move, with no other forces present, the E field is doing negative work, slowing the mass

 

[lys04]

That slide is quite misleading. It doesn't specify which work is being considered as positive or negative, the work done by the field or the work done by the external force.

Better would be:

• If a charge is moving in the direction it would naturally move, the E field is doing positive work
• If a charge is moving opposite to the direction it would naturally move, the E field is doing negative work

There might or might not be an external force. If the speed is constant there must be one and we can add:

• If a charge is moving in the direction it would naturally move, the external force is doing negative work
• If a charge is moving opposite to the direction it would naturally move, the external force is doing positive work

Or if no other force is present then the speed must be changing and the charge must have mass:

• If a charged mass is moving in the direction it would naturally move, with no other forces present, the E field is doing positive work accelerating the mass
• If a charged mass is moving opposite to the direction it would naturally move, with no other forces present, the E field is doing negative work, slowing the mass

 

[lys04]

Ohh ok, yeah this is much clearer. Thanks. But why would a charge just move in the opposite direction it will naturally move without an external force?

 

[haruspex]

Ohh ok, yeah this is much clearer. Thanks. But why would a charge just move in the opposite direction it will naturally move without an external force?

It would not do so from rest, but some force could have sent it that way then ceased to act, leaving it to continue under its own momentum. The charged mass slows as it does positive work against the field.

 

[lys04]

It would not do so from rest, but some force could have sent it that way then ceased to act, leaving it to continue under its own momentum. The charged mass slows as it does positive work against the field.

Oh ok, I understand. So then work done by E field = -Work done by charge?

 

[haruspex]

Oh ok, I understand. So then work done by E field = -Work done by charge?

Yes.

 

[kuruman]

Oh ok, I understand. So then work done by E field = -Work done by charge?

I would phrase it somewhat differently. The charge is the system and work is done on it by external forces. Prepositions are important and the system (charge) cannot do work on itself.

If the charge moves at constant velocity in an electric field then the net force on it is zero. The work done by the electric field on the charge is the negative of the work done by the external agent on the charge. This is the case regardless of whether the charge is moving in the same or in the opposite direction as the field.

Say the charge would "naturally move" to the right if the electric field were the only force acting on it. This means that the electric field does positive work on the charge if it is moving to the right and negative work if it is moving to the left.

Imagine the charge being held by a hand and moving to the right at constant velocity. "Naturally", the charge would accelerate to the right but the acceleration is zero. The electric field does positive work and the hand does negative work on the charge so that the net work is zero. The electric field acts as if it were an accelerator while the hand acts as if it were a brake.

Now imagine the charge being held by the hand and moving to the left at constant velocity. "Naturally", the charge would accelerate to the right but the acceleration is zero. The electric field does negative work and the hand does positive work on the charge so that the net work is zero. The hand acts as if it were an accelerator while the electric field acts as if it were a brake.

The symmetry in exchanging the roles that the external forces play is guaranteed by Newton's third law.

 

[lys04]

I would phrase it somewhat differently. The charge is the system and work is done on it by external forces. Prepositions are important and the system (charge) cannot do work on itself.

If the charge moves at constant velocity in an electric field then the net force on it is zero. The work done by the electric field on the charge is the negative of the work done by the external agent on the charge. This is the case regardless of whether the charge is moving in the same or in the opposite direction as the field.

Say the charge would "naturally move" to the right if the electric field were the only force acting on it. This means that the electric field does positive work on the charge if it is moving to the right and negative work if it is moving to the left.

Imagine the charge being held by a hand and moving to the right at constant velocity. "Naturally", the charge would accelerate to the right but the acceleration is zero. The electric field does positive work and the hand does negative work on the charge so that the net work is zero. The electric field acts as if it were an accelerator while the hand acts as if it were a brake.

Now imagine the charge being held by the hand and moving to the left at constant velocity. "Naturally", the charge would accelerate to the right but the acceleration is zero. The electric field does negative work and the hand does positive work on the charge so that the net work is zero. The hand acts as if it were an accelerator while the electric field acts as if it were a brake.

The symmetry in exchanging the roles that the external forces play is guaranteed by Newton's third law.

Thanks for clearing it up! I just have 2 questions tho, why would the net charge be 0 in this case if the charge is moving to the left? Also I guess in this case it’s pretty cool that there is work done individually by both the E field and the hand although the charge is not moving since W=Fd but neither the hand or the E field is moving the charge.

 

[lys04]

It's often better to ask only one question at a time. Or answers /conversations about different questions get muddled-up with each other. However...Consider the case where $Q_1$ and $Q_2$ are both positive. A leftwards external force ($\vec F_{ext}$) is applied to $Q_2$, moving it leftwards towards $Q_1$. $\vec F_{ext}$ and its displacement are in the same direction (both to the left, both negative) and their dot product is therefore positive. The work done by $\vec F_{ext}$ is positive.

Energy has been supplied by $\vec F_{ext}$ and this has increased the system’s potential energy,

(Note that the work done done by the electric force, $\vec F_E$, is negative. This work is minus the charge in potential energy. This is may be easiest to understand by considering gravity. If you drop a stone, gravity does positive work (providing kinetic energy); as a consequence, the change in gravitational potential energy is negative.)That's not a question . And it's not accurate. If you have a spherically symmetric charge distribution (e.g. a uniformly charged sphere), then outside the distribution, the field is identical to that produced by point charge of the same magnitude positioned at the centre of the distribution.See above.If the potential is constant (though not necessarily zero) the electric field is zero. Can you see how that answers your question?

Oh ok, so V=kq/r applies for both point charges and spherical conductors with uniform distribution but for surface and outside only?

 

[haruspex]

but for surface and outside only?

That depends on how you define r. If you define it as the greater of

• the radius of the sphere
• the distance from the centre of the sphere to the point in question

then it is true in general.

 

[lys04]

That depends on how you define r. If you define it as the greater of

• the radius of the sphere
• the distance from the centre of the sphere to the point in question

then it is true in general.

Sorry I didn’t quite understand what you mean by “the greater of”?

 

[haruspex]

Sorry I didn’t quite understand what you mean by “the greater of”?

The one with the larger value. If the point at which the potential is wanted is at $r_p$ from the sphere's centre and the radius of the sphere is $r_s$ then the potential is $kq/r$ where $r=\max(r_p,r_s)$.

 

[jbriggs444]

Oh ok, so V=kq/r applies for both point charges and spherical conductors with uniform distribution but for surface and outside only?

A problem trying to apply this principle to objects that are conductive is that the charge on a conductive object will rearrange itself when acted on by an electric field. The charge distribution of the conductive object will then no longer be uniform.

For instance, a negatively charged spherical balloon can induce a dipole on a neutral (or even a slightly negatively charged!) conductive balloon and then attract it.

 

[lys04]

The one with the larger value. If the point at which the potential is wanted is at $r_p$ from the sphere's centre and the radius of the sphere is $r_s$ then the potential is $kq/r$ where $r=\max(r_p,r_s)$.

Got it! Thanks a lot. :)

 

[lys04]

A problem trying to apply this principle to objects that are conductive is that the charge on a conductive object will rearrange itself when acted on by an electric field. The charge distribution of the conductive object will then no longer be uniform.

For instance, a negatively charged spherical balloon can induce a dipole on a neutral (or even a slightly negatively charged!) conductive balloon and then attract it.

This means that it can only be applied to conducting objects that are isolated? Away from any external E fields?

 

[jbriggs444]

This means that it can only be applied to conducting objects that are isolated? Away from any external E fields?

It can be applied to non-conducting objects that are uniformly charged [or which have a spherically symmetric charge distribution].

It can be applied, approximately, to conducting objects as long as the external field is weak so that the charge distribution remains approximately uniform.

 

[kuruman]

$\dots~$ why would the net charge be 0 in this case if the charge is moving to the left?

The net charge is not zero. The net work is zero. That's because the charge is moving with constant velocity by assumption. According to the work-energy theorem the change in kinetic energy of the charge is equal to the total work done on the charge. If the kinetic energy does not change, this total work is zero.

Also I guess in this case it’s pretty cool that there is work done individually by both the E field and the hand although the charge is not moving since W=Fd but neither the hand or the E field is moving the charge.

Where did you get this idea? The charge is indeed moving at constant velocity. Please reread post #12.

 

[lys04]

The net charge is not zero. The net work is zero. That's because the charge is moving with constant velocity by assumption. According to the work-energy theorem the change in kinetic energy of the charge is equal to the total work done on the charge. If the kinetic energy does not change, this total work is zero.

Where did you get this idea? The charge is indeed moving at constant velocity. Please reread post #12.

The net charge is not zero. The net work is zero. That's because the charge is moving with constant velocity by assumption. According to the work-energy theorem the change in kinetic energy of the charge is equal to the total work done on the charge. If the kinetic energy does not change, this total work is zero.

Where did you get this idea? The charge is indeed moving at constant velocity. Please reread post #12.

Sorry yeah I was meant to type work, I understand now! Thanks a lot.