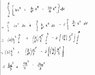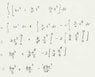Eliminate constants/Moment of Inertia

[aaronfue]

Homework Statement

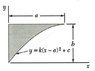
Find the moment of inertia, Iy, about the y-axis using a vertical strip, width dx.
Use the given equation and eliminate constants k and c, express answer in terms of number and powers of a and b.

Homework Equations

I can't figure out how to eliminate the constants k and c?

The Attempt at a Solution

I believe I have the integration ready:

\int^{a}_{0} x^{2} (b-y)dx
where y=k(x-a)² + c

 

[gneill]

I can't figure out how to eliminate the constants k and c?

Pick out two points on the curve where you know the coordinates. Use these values to obtain two equations in two unknowns (c and k).

 

[aaronfue]

Ok. So far this is what I have:

I know the point at the origin (0,0). And x=a and y=b.

0 = k(0 - a)² + c = ka² + c ==> k = -\frac{c}{a^2}

So,

y=(-\frac{c}{a^2})(x-a)² + c

I'm still not sure how to get rid of the c?

 

[gneill]

Start with your second known point.

 

[aaronfue]

I see... so x=a, y=b

b=(-\frac{c}{a^2})(a-a)² + c
b=(-\frac{c}{a^2})(0)² + c
b=c

...I think??

 

[gneill]

I see... so x=a, y=b

b=(-\frac{c}{a^2})(a-a)² + c
b=(-\frac{c}{a^2})(0)² + c
b=c

...I think??

Yup. So replace c in the y(x) function and then plug in the (0,0) point to see what k is all about...

 

[aaronfue]

Yup. So replace c in the y(x) function and then plug in the (0,0) point to see what k is all about...

Thanks! Would you also check if my integration is set up correctly?

\int^{a}_{0} x² [b-(\frac{-b}{a^2})(x-a²) + b] dx

How would I get my answer in terms of a number and powers of constants a and b (per instructions)?

 

[gneill]

Thanks! Would you also check if my integration is set up correctly?

\int^{a}_{0} x² [b-(\frac{-b}{a^2})(x-a²) + b] dx

How would I get my answer in terms of a number and powers of constants a and b (per instructions)?

For your integration, be sure that you're squaring the right thing in the integrand; is it just "a" that is squared?

Once you perform the integration the result will be in terms of a constant and powers of a and b.

Note that the tacit assumption is that the 'material' that the figure is made of has a uniform density of 1 mass unit per unit area. If instead you want to assume a mass M for the object, you should calculate its density from M and the total area and incorporate this into the determination of the moment of inertia.

 

[aaronfue]

For your integration, be sure that you're squaring the right thing in the integrand; is it just "a" that is squared?

Once you perform the integration the result will be in terms of a constant and powers of a and b.

Note that the tacit assumption is that the 'material' that the figure is made of has a uniform density of 1 mass unit per unit area. If instead you want to assume a mass M for the object, you should calculate its density from M and the total area and incorporate this into the determination of the moment of inertia.

I thought that the equation for Iy was

∫_A x² dA

Why would the "a" be the only thing squared?

 

[gneill]

Isn't the function $-\frac{b}{a^2}(x - a)^2 + b$, so that it's the whole term $(x - a)$ that's squared, not just the a in the term?

 

[aaronfue]

Isn't the function $-\frac{b}{a^2}(x - a)^2 + b$, so that it's the whole term $(x - a)$ that's squared, not just the a in the term?

My answer came out to be:

\frac{3ba^3}{10}

I don't understand how to get a power of a constant with this problem?

 

[gneill]

a and b are constants. So in your answer b is to the power of 1 and a is to the power of 3.

The numerical constant 3/10 looks off to me though. Can you show more detail in your work?

 

[aaronfue]

a and b are constants. So in your answer b is to the power of 1 and a is to the power of 3.

The numerical constant 3/10 looks off to me though. Can you show more detail in your work?

I've attached a scan of my work. Now that I've looked at the problem, I think I left out a "b-" for my "ydx". I think that it should be (b-y)dx. Seem right?

 

[gneill]

I've attached a scan of my work. Now that I've looked at the problem, I think I left out a "b-" for my "ydx". I think that it should be (b-y)dx. Seem right?

Yup. b-y(x) is the length of the differential strips.

 

[aaronfue]

Yup. b-y(x) is the length of the differential strips.

After including "b-" in my problem my answer came out to be:

\frac{8ba^3}{15} - \frac{2ba}{3},

without factoring.

Radius of Gyration: K_y = \sqrt{\frac{(\frac{8ba^3}{15} - \frac{2ba}{3})}{(b-y)dx}}

 

[gneill]

Your integral should look something like:

$$\int_0^a x^2\left[ b - \left[-\frac{b}{a^2}*(x - a)^2 +b\right]\right]dx$$
$$= \int_0^a x^2\left[\frac{b}{a^2}(x - a)^2\right]dx$$
$$= \int_0^a b x^2 - 2\frac{b}{a}x^3 + \frac{b}{a^2}x^4 \, dx$$

Evaluating the last form term by term should leave you with terms having b to the power of one, a to the power of three only. Try the integral again.

 

[aaronfue]

Your integral should look something like:

$$\int_0^a x^2\left[ b - \left[-\frac{b}{a^2}*(x - a)^2 +b\right]\right]dx$$
$$= \int_0^a x^2\left[\frac{b}{a^2}(x - a)^2\right]dx$$
$$= \int_0^a b x^2 - 2\frac{b}{a}x^3 + \frac{b}{a^2}x^4 \, dx$$

Evaluating the last form term by term should leave you with terms having b to the power of one, a to the power of three only. Try the integral again.

I see what I did wrong. Instead of having (-\frac{2b}{a}x³), I had: (-\frac{2b}{a^2}x³).

I now have: ba²*(\frac{8ba}{15} - \frac{2}{3})??

I believe I integrated correctly.

 

[gneill]

I see what I did wrong. Instead of having (-\frac{2b}{a}x³), I had: (-\frac{2b}{a^2}x³).

I now have: ba²*(\frac{8ba}{15} - \frac{2}{3})??

I believe I integrated correctly.

If that's your result for the integration, it's not correct. Integrate term by term and show your work.

 

[aaronfue]

Here is the new integration that I did. I didn't know if I should leave it as is or try to simplify it. There are no instructions that say to do so.

 

[gneill]

In the first line of your attachment, the term with the coefficient -2b/a should be an x³ term, not x². There's one x² term, one x³ term, and one x⁴ term going into the integration.

 

[aaronfue]

In the first line of your attachment, the term with the coefficient -2b/a should be an x³ term, not x². There's one x² term, one x³ term, and one x⁴ term going into the integration.

Dang...I see! After I distributed the x² I didn't apply it to that part.

 

[aaronfue]

Alright...

After re-distributing the x² into my (b-y)dx, I got the answer that is in the image attached.

I guess I could factor out the ba³ and add/subtract fractions...

 

[gneill]

Yup. Simplify the result.

 

[aaronfue]

Great.

Now all I have to do is figure out the same answer using a horizontal strip (dy)!? I'm guessing, solve the equation as "x=" and plug that in?

Use: \frac{x^3}{3}dy

 

[gneill]

Great.

Now all I have to do is figure out the same answer using a horizontal strip (dy)!? I'm guessing, solve the equation as "x=" and plug that in?

Use: \frac{x^3}{3}dy

Ouch. That might be a bit nasty; your x(y) function is going to involve a radical.

Well, show us what you get

 

[aaronfue]

Ouch. That might be a bit nasty; your x(y) function is going to involve a radical.

Well, show us what you get

I was given a suggestion to substitute the expression for dy in terms of x and dx then integrate over the limits of x (0 to a).

Also to use \frac{x^3}{3}dy

Here is what I did:

I took the derivative of my function to get my "dy":

dy = -\frac{2bx}{a^2} + \frac{2b}{a} dx

Then I integrated that to get my final answer of \frac{ba^3}{30}, which was the same as I initially got.

 

[gneill]

Hey, there's no arguing with success