chipotleaway
- 174
- 0
Homework Statement
Eliminate the denominator on the RHS of the following expression
sin(\alpha)-sin(\beta) = -\frac{-v(sin(\alpha) cos(\alpha) + sin(\alpha) cos(\beta)}{c-vcos(\alpha)}
and from it, derive
sin(\alpha)-sin(\beta) = -\frac{v}{c}(sin(\alpha)cos(\beta)+sin(\beta)cos(\alpha))
Homework Equations
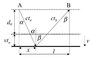
For a bit of context, this is from a multipart derivation of the relativistic reflection law based on the principle of least time. I'm assuming that you don't need to know what the sines and cosines in terms of the lengths of the triangles because the hint says to 'multiply through' (and substituting back in lengths hasn't made it any better), but I've attached the diagram I'm working from anyway.
The Attempt at a Solution
Some things I've tried:
- worked backwards from the RHS expression in the second equation to see if I could find what to multiply by
- multiplied by top and bottom by c+vcos(\alpha)
- tried writing sin(\alpha) and cos(\alpha) as the ratios of the lengths in hopes of getting a sin(\beta) and [/itex]sin(\alpha)[/itex] back out of it. This is what I got:
-\frac{v}{c}(\frac{x(cos(\alpha)+cos(\beta))}{\sqrt{(d_0+vt_a)^2+x^2)}-v(d_o+vt_a)})
--