Ellipse Collisions: Resolving the Paradox

[nuclearhead]

I have a paradox here.

Look at this diagram of colliding ellipses (they might be elliptical prisms in 3D). Now if you stretch the image (for example looking at the image from an angle) it becomes two colliding circles. Therefore you would expect by that argument that the colliding force would be applied through the centres of the ellipses (yellow line).

But another argument says that looking close up at where the ellipses collide it is like two colliding planes and the force should be perpendicular to that (orange line). And this would cause the ellipses to rotate.

So which is right? And will the ellipses be rotating after the collision?

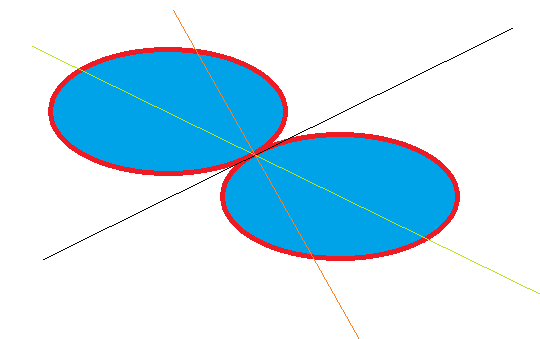
I have not found any equations for colliding ellipses as there are with colliding circles.

 

[A.T.]

the force should be perpendicular to that (orange line).

If the surfaces are friction-less.

 

[nuclearhead]

If the surfaces are friction-less.

But aren't the Newton's laws invariant under scaling of a coordinate axis?

 

[Vatsal Sanjay]

But aren't the Newton's laws invariant under scaling of a coordinate axis?

Yes they are.
Exactly at what angle do you expect to see these as circles? Is it not possible that at that angle these two lines (orange and yellow as you mentioned) coincide? (*Just a guess). It would be of great help if you can explain exactly what angle are you talking about?

Whenever there is a collision and the surfaces are frictionless, the normal contact force acts perpendicular to the surfaces in contact because if it is not; then there will be a component of the force in the tangential direction which is not possible as the surfaces are frictionless.

 

[nuclearhead]

Yes they are.
Exactly at what angle do you expect to see these as circles? Is it not possible that at that angle these two lines (orange and yellow as you mentioned) coincide? (*Just a guess). It would be of great help if you can explain exactly what angle are you talking about?

Whenever there is a collision and the surfaces are frictionless, the normal contact force acts perpendicular to the surfaces in contact because if it is not; then there will be a component of the force in the tangential direction which is not possible as the surfaces are frictionless.

That's what I mean. If you stretch the image so they are both circles, the orange line is no longer perpendicular.

Isn't that strange? I mean shouldn't contact force be the same if you stretched the image? Where has my logic gone wrong?

 

[Vatsal Sanjay]

If you stretch the image so they are both circles

Are you suggesting we change the figure? If you stretch or do something with you current surfaces, you will get "new" surfaces. In that case your eclipses are no longer eclipses. See there is a difference between rotating your current figure and looking at it at different angles and stretching or shrinking the figure to obtain new surface. In the latter case, the normal force will be perpendicular to the new tangent of the surface in contact.

 

[A.T.]

I mean shouldn't contact force be the same if you stretched the image?

If you stretch an incline horizontally, is the direction of a normal force on it still the same?