(empirical) relation between MSE and condition number

[divB]

Hi,

It is a well known fact that in an inverse linear problem low condition numbers have low noise amplification and therefore decrease the error.

So I wanted to test this: I draw random (skinny) matrices A, calculate y=A*c where c is a known coefficient vector, add some noise and calculate c from Least Squares. I would expect at least a small correlation between the MSE for c and the condition number.

But this is what it looks:

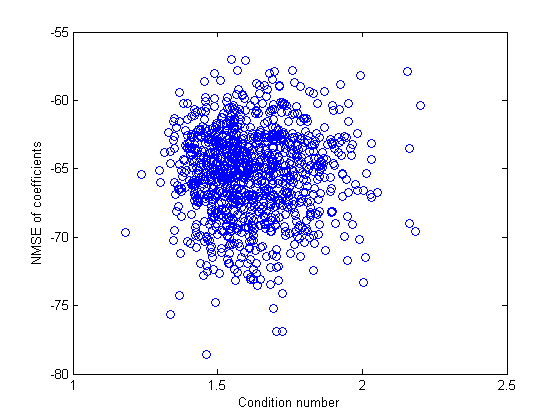
Yes, is it arbitrary, uncorrelated, this does not make sense at all! For example, a (relatively) low condition number of 1.5 can produce everything from the best (-79dB) down to the worst (-56dB). Changing the parameters does not change anything

Can anyone tell me what I am doing wrong or which (wrong?) assumptions I make?

Thanks


PS: Here is the MATLAB code

K = 5;
M = 50;
numtrials = 1000;
c = randn(K,1);
for trial=1:numtrials
    A = randn(M,K);
    y = A*c;
    y = add_noise(y, 55); % add 55dB noise via randn(...)
    c_rec = A \ y; %c_rec = pinv(A)*y;
    NMSE_c = 20*log10(norm(c - c_rec)/norm(c));
    plot(cond(A), NMSE_c, 'bo');
    hold on;
    xlabel('Condition number');
    ylabel('NMSE of coefficients');
    drawnow;
end

 

[coquelicot]

Well, this is not my field but I will try to give you some advices. What's happen if you add a 0db noise ? Also, are you sure that the function add_noise is bug free ?