Energy and momentum + radioactive decay

[imphat]

Homework Statement

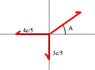
Let's consider a radioactive decay according to the attached figure. A particle of initial mass M and charge Q is resting according to a referential R and disintegrates itself on 3 identical particles. As shown in the picture, 2 of the particles have known speeds 4c/5 and 3c/5 and the other one has speed unknown.

We want to know:

a) what's the charge q of each of the new particles?
b) what's the value of the angle A?
c) what's the value of M/m, where m is the the mass of one of the new particles?

Homework Equations

The Attempt at a Solution

I can calculate the x and y components for the 3rd particle speed vector and find out what's the value of A, but I'm not pretty sure how to add the charged Q and q into account while handling with energy or momentum conservation.
Same goes for the new charge q. The exercise says that each of these new particles do have the same charge value q, but I don't know how that value is related to Q.
Any help? :D

 

[tiny-tim]

Welcome to PF!

I can calculate the x and y components for the 3rd particle speed vector and find out what's the value of A, but I'm not pretty sure how to add the charged Q and q into account while handling with energy or momentum conservation.
Same goes for the new charge q. The exercise says that each of these new particles do have the same charge value q, but I don't know how that value is related to Q.

Hi imphat! Welcome to PF!

For q, just use conservation of charge: total charge before = total charge after.

For m, I don't think you bother about charge - the velocities are measured "at infinity".

 

[imphat]

hello, and thanks for your reply

part a
so, since there is a charge conservation and all 3 new particles are identical then the new charge of each particle is q = Q/3. part b
now, about the angle A, since momentum is conserved, and assuming that, after the decay, the particle 1 has momentum p1=m1.v1, can i say that the particle 3 has, in the x-axis, momentum p3x = -p1?

then p3x = m3.v3x and similarly p3y = m3.v3y = (-1).m2.v2, right?

so i got
| m3.v3y | = | m2.v2 |
| m3.v3x | = | m1.v1 |
v3^2 = v3x^2 + v3y^2

where
v1 = 4c/5
v2 = 3c/5
mi = m/sqrt(1-vi^2/c^2)

is that correct? part c
also, i don't get the last question of the problem. It states that each of the new particles has a new resting mass mo = m and asks for M/m. if, from b) i get the v3 value, what do i have to do? I was thinking using energy conservation, so

E = Mc^2 = 3m.c^2 + m1.v1^2 + m2.v2^2 + m3.v3^2

Would that be right?

 

[tiny-tim]

… relativistic momentum …

Hi imphat!

Part a: Yes.

Part b: That would be fine for ordinary velocities.

But the question obviously wants you to take relativity into account.

(Otherwise v3 would be c√(.6^2 + .8^2), = speed of light, wouldn't it?!)

So your momentum equations must use the relativistic form of momentum.

Try again …

 

[imphat]

i see, so i used this

- before the decay
px = initial total momentum on x-axis = 0
py = initial total momentum on y-axis = 0- after the decay
px = p1x + p3x

p1x = p1 = m.g1.v1
where
g1 = 1 / √(1 - (v1^2 / c^2) )

p3x = m.g3.v3x
where
g3 = 1 / √(1 - (v3^2 / c^2) )

ie, I'm considering the relativistic mass on the momentum formulas.
then, since the initial momentum was 0, it means that, in module, p1 and p3x are the same

| p1 | = | p3x |

same thing goes for p2 and p3y and after some math i got that

p3y / p3x = 9/16, so

A = arctg 9/16

is that correct?
what about the last part? should i use the energy conservation idea or is there another way?
the problem with using the energy conservation is that, for part B i never had to actually do the math and find out v3. All i have to do is find the ratio v3y/v3x.

 

[tiny-tim]

p3y / p3x = 9/16, so

A = arctg 9/16

is that correct?

Yes!

No, you don't need any more physics to find the velocity … its just maths from now on … you have momentum in both x and y directions … Pythagoras gives you total momentum … you just need to solve for v3 in momentum = v3/√(1 - v3^2/c^2).