Gamdschiee said:
@Pablo L Martin
But I do not get the origin from such standing wave. Does it come from the waves with wave vector ##\vec k## and ##\vec k - \vec G## ?
Or can you only say in a 1D crystal that a wave traveling to the right with wavevector k = \pi/a (zone edge in reciprocal space) gets reflected in a wave traveling to the left and so there must be a standing wave in the real crystal.
For this simple 1D case, a wave traveling to the right will reflect to the left if it meets Bragg's condition, which corresponds to ##k=\frac{\pi}{a}##. Since Bragg scattering is an elastic process and we are constrained to 1D, the scattered wave will bounce directly backward with ##k' = -\frac{\pi}{a}##. This can also be worked out mathematically by applying your above stated Bragg equation ##\mathbf k' = \mathbf k + \mathbf G##. It is the superposition of the
same electron's initial and scattered wave function that sets up the standing waves. You can generate the standing waves from the initial and final plane wave function ##\exp(\pm i\pi x/a)##. This is how you get the standing waves of form:
##\psi(+) = \exp(i\pi x/a) + \exp(-i\pi x/a) = 2\cos(\pi x/a)##
##\psi(-) = \exp(i\pi x/a) - \exp(-i\pi x/a) = 2i\sin(\pi x/a)##
If you want to visualize this more clearly in your mind in terms of classical standing waves, then the Brillouin zone boundary ##k = \frac{\pi}{a}## corresponds to a wave traveling down a string with wavelength ##\lambda = \frac{2\pi}{k} = 2a## where the lattice spacing ##a## is now just the distance between the endpoints of the string. ##\psi(+)## corresponds to both endpoints free (which sets up a node centered between the endpoints) while ##\psi(-)## corresponds to both endpoints fixed (which sets up nodes at the endpoints). Note that one end fixed and one end free is not allowed because this requires meeting the condition that ##a = \frac{n\lambda}{4}## where n is an odd integer. However, since Bragg's condition requires ##\lambda = \frac{2a}{m}## where m is any positive integer, then combining these conditions gives ##n = \frac{2}{m}##. Hence, no odd integer n exists.
Gamdschiee said:
@Pablo L Martin
Because in 3D etc the diffracted wave could be go anywere. This is hard to understand. Can anyone help me with this please?
In higher dimensions nothing much has changed. As an elementary example consider an electron with ##\mathbf k = k_{x} \hat {\mathbf x} + k_{y} \hat {\mathbf y}## that hits a reciprocal lattice vector ##\mathbf G = -\frac{2\pi}{a} \hat {\mathbf x}##. Thus, we have that ##\mathbf k' = \mathbf k + \mathbf G = (k_{x}-\frac{2\pi}{a} ) \hat {\mathbf x} +k_{y}\hat {\mathbf y}##. From the Bragg condition ##k^{2} = |\mathbf k + \mathbf G|^{2}## we get that ##k_{x} = \frac{\pi}{a} ## an so taken together
##\mathbf k = \frac{\pi}{a} \hat {\mathbf x} + k_{y} \hat {\mathbf y}##
##\mathbf k' = -\frac{\pi}{a} \hat {\mathbf x} + k_{y} \hat {\mathbf y}##
Note that the since ##\mathbf G## is along the x-direction, the Bragg condition required ##k_{x}## to be a specific value. However, ##k_{y}## is allowed to remain arbitrary. Thus, the diffracted beam in higher dimensions is not free to go anywhere, there is a direct bounce back (like in 1D) for the momentum projection along ##\mathbf G##. The upshot of this is that now when we put together the superposition of our initial and final plane waves we get that
##\psi(+) =\exp(ik_{y}y) \left( \exp(i\pi x/a) + \exp(-i\pi x/a)\right) = 2\exp(ik_{y}y)\cos(\pi x/a)##
##\psi(-) = \exp(ik_{y}y) \left( \exp(i\pi x/a) - \exp(-i\pi x/a)\right) = 2i\exp(ik_{y}y)\sin(\pi x/a)##
So we see that an arbitrary phase is added into the standing wave solution. However, the electron density is given by the modulus and so this arbitrary phase disappears.
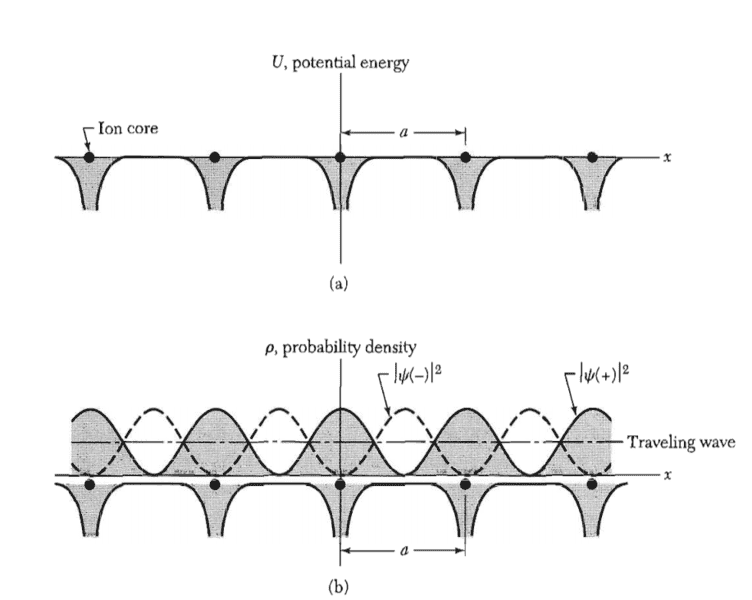
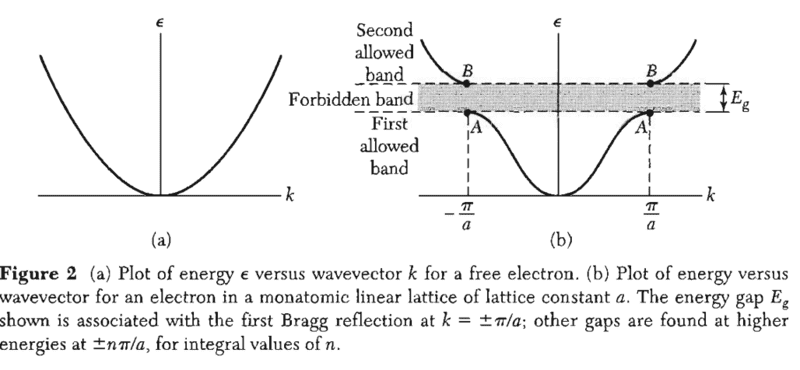 It says that the first energy gap(which we see here between band 1 and band 2) occurs due to the bragg reflection at ##k = \pi/a## and ##k = - \pi/a##. The book from Kittel (Solid Sate Physics) also says:
It says that the first energy gap(which we see here between band 1 and band 2) occurs due to the bragg reflection at ##k = \pi/a## and ##k = - \pi/a##. The book from Kittel (Solid Sate Physics) also says: