Energy Principle for Motion in Space

[NotanEngineer]

Homework Statement

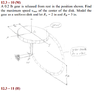
A 0.2 lb gear is released from rest in the position shown (Okay so this essentially a circular gear in the groves on an adjacent wall that is also circular. Think perpendicular circles with different radii. The gear is a circle, and the gear teeth are in a circular pattern; the picture is attached) Find the maximum speed of the center of the disk and let the radius of the gear be 2 inches. And the radius of the path is 3 inches.

Homework Equations

2nd energy Principle: E1= V1 +T_t1 + T_r1 = E2 = V2 + T_t2 + T_r2
V= mgh T_t= 1/2mv^2 T_r= 1/2 ω$\bullet$ [Ic] $\omega$

The Attempt at a Solution

My attempt was to treat the path around the wall as translational, and keep the disk spinning around the center as rotational energy. The problem I'm having is I don't really know how to configure my omega or the moments of inertia. I think my biggest issue is setting the coordinate system, and defining all of the parts that go into the equations that will eventually be put into my relevant energy equations.

 

[mfb]

The problem I'm having is I don't really know how to configure my omega or the moments of inertia.

You can split it in the rotation of the disk around its center and the rotation around the horizontal axis. It is possible to split up the latter into a translation and another rotation around the center of the disk, but that won't change much.

This should also give a start how to calculate the corresponding moments of inertia.
The angular velocites are linked via the teeth in the wall.

 

[NotanEngineer]

Okay so my total kinetic energy is going to be the rotational kinetic energy for the disk about itself plus the rotational kinetic energy for the disk about the center. That's beautiful.

Last question. Would it be acceptable to model the disk as a point particle moving around the in a circle. Otherwise I wouldn't know how to calculate the moment(s) of inertia.

 

[mfb]

Would it be acceptable to model the disk as a point particle moving around the in a circle

Is it a point particle?

Otherwise I wouldn't know how to calculate the moment(s) of inertia.

There are formulas for disks rotating around the two different relevant axes, but it is possible to calculate it directly via integration as well.