vbtweakin
- 3
- 0
the problem states as this
it's a energy related problem
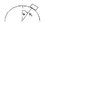
A sled starts from rest at the top of the frictionless, hemispherical snow-covered hill.
a)Find an expression for the sled's speed when it is at angle "theta"
b)Use Newton's laws to find the maximum speed the sled can have at angle "theta" without leaving the surface.
c)at what angle "theta"max does the sled "fly off" the hill?
since the surface is fristionless the energy is conserved we can say E at start = E at angle theta
now i realize at the top the sled has zero kinetic energy and Pe=mgR
and the at point "thete" Ke=1/2mV^2 and Pe=mgh
now at this point I am stuck and not sure what to do with all this data
thanks in advance
it's a energy related problem
A sled starts from rest at the top of the frictionless, hemispherical snow-covered hill.
a)Find an expression for the sled's speed when it is at angle "theta"
b)Use Newton's laws to find the maximum speed the sled can have at angle "theta" without leaving the surface.
c)at what angle "theta"max does the sled "fly off" the hill?
since the surface is fristionless the energy is conserved we can say E at start = E at angle theta
now i realize at the top the sled has zero kinetic energy and Pe=mgR
and the at point "thete" Ke=1/2mV^2 and Pe=mgh
now at this point I am stuck and not sure what to do with all this data
thanks in advance