elemis
- 162
- 1
My professor, in his handout (picture below), says the following about this diagram :
I disagree with him partly. For \Delta_{mix} G/nRT<0 mixing is spontaneous and hence there solutions would be miscible. Hence at \beta=2.5 should we not expect the components to be fully miscible. ?
Following on from this logic; for \beta=3 the components are only miscible for \Delta_{mix} G/nRT<0 so the maxima represents a phase separation between the two components.
Who is correct ?
Additionally,the webpage below indicates that at the maxima there is one phase whilst at the minima there are two. Does this mean at the maxima the solutions are miscible ? If so, how can this be true given that \Delta_{mix} G/nRT<0 is positive and hence mixing is unfavourable ?
http://www.chm.bris.ac.uk/~chdms/Teaching/Chemical_Interactions/page_17.htm
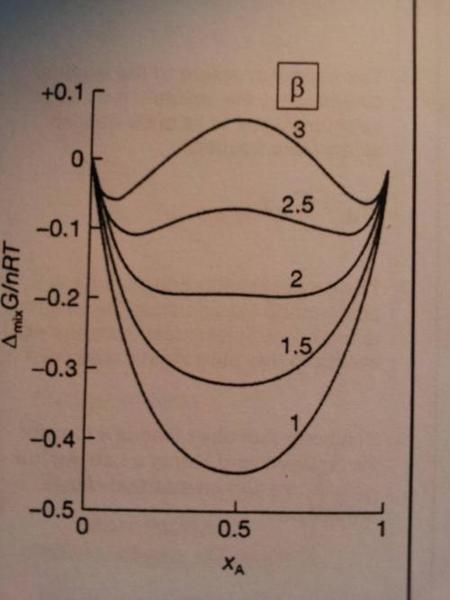
For \beta>+2 there are two minima and phase separation occurs driven
by unfavourable enthalpic interactions.
I disagree with him partly. For \Delta_{mix} G/nRT<0 mixing is spontaneous and hence there solutions would be miscible. Hence at \beta=2.5 should we not expect the components to be fully miscible. ?
Following on from this logic; for \beta=3 the components are only miscible for \Delta_{mix} G/nRT<0 so the maxima represents a phase separation between the two components.
Who is correct ?
Additionally,the webpage below indicates that at the maxima there is one phase whilst at the minima there are two. Does this mean at the maxima the solutions are miscible ? If so, how can this be true given that \Delta_{mix} G/nRT<0 is positive and hence mixing is unfavourable ?
http://www.chm.bris.ac.uk/~chdms/Teaching/Chemical_Interactions/page_17.htm
Last edited by a moderator: