Okay, I think this is it. There are
two different definitions of strain,
true strain ##\tilde{\varepsilon}## defined by ##d\tilde{\varepsilon} = \frac{dL}{L} \implies \tilde{\varepsilon} = \ln{(1+\frac{\Delta L}{L})} = \ln{(1+\varepsilon)}##, and also the
engineering strain, which is defined by the more familiar relation ##d\varepsilon = \frac{dL}{L_0} \implies \varepsilon = \frac{\Delta L}{L_0} = \frac{L-L_0}{L_0}##. The
engineering strain is much more common, and is used in the definition of the Young modulus ##\sigma = Y\varepsilon##. But for infinitesimal strains, ##\tilde{\varepsilon} \approx \varepsilon## and the Young modulus is$$Y = \underbrace{\frac{L_0}{A} \left( \frac{\partial F}{\partial L} \right)_T}_{\text{w/ engineering strain}} \approx \underbrace{\frac{L}{A} \left( \frac{\partial F}{\partial L} \right)_T}_{\text{w/ true strain}}$$So I believe the equation quoted in Finn is valid as an approximation in the limit of small strains.
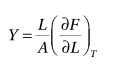
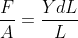 , i don't think we can say this definition and the first definition is equal.
, i don't think we can say this definition and the first definition is equal.