Automotive Equation of motion for a driving wheel

[Payam30]

Hi,
I have a Driving wheel for which I'm trying to make an observer for. The abserver works very well however , since I don't have my background in mechanics something strange happens. I have to say that I don't know why I think it's strange and that's why I put my question here.
Lets assume we have a driving wheel. The traction force is in the direction of motion and so is the rolling resistance since we have a driving wheel.

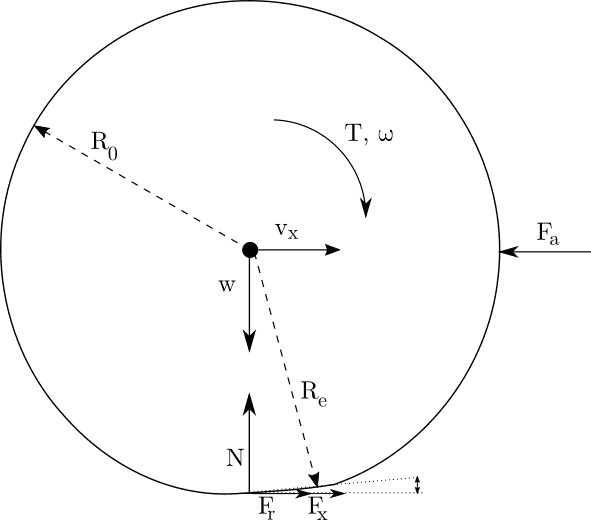
The EOM would be
J \dot{\omega} = T- F_r R_e - F_x R_e
m \dot{v} = F_x + F_r
here we assume that the values of F_s are neglectable.
In the figure N,W, R_e, F_r, F_x, F_a, T, \omega, R_0 are Normal force, weight, effective radius, Rolling resistance, traction force, aerodynamic force, torque, angular velocity, and nominal tire radius.
When I try to solve for \omega for this system with, T = 100-400 Nm, F_x = 0.6*700*9.81 N, F_r = 127- 173 N, J = 25.1 , m = 700 kg, R_e = 0,72 m, F_a = 0 N I get negative values for \omega =0:-550 rad/s and velocity to v = 0-32 m/s. how can it be possible? where am I doing wrong? why is \omega negative and translation velocity positive?

 

[BvU]

Hi,
Could it be as simple as: a positive $\omega$ is counterclockwise ? (and a positive torque $T$ as well...)

 

[Payam30]

I have

Hi,
Could it be as simple as: a positive $\omega$ is counterclockwise ? (and a positive torque $T$ as well...)

no idea. However 400 rad/s is very high. $\omega$ should the sam direction as torque

 

[BvU]

However 400 rad/s is very high

I agree. So is -550.
But, just like the other numbers, to me they come out of the blue sky.

If they come from your second relevant formula, however, they are definitiely wrong: there is no way a momentum and a force can be equal. They simply don't have the same dimension. What is it you mean to say with $m \dot{v} = F_x + F_r$ ?

[edit]Sorry, missed the dot.

In your first formula you write $T$ and $F_x\,R_e$ on one side with opposite signs. You sure this is the equation of motion ? Aren't $T$ and $F_x\,R_e$ one and the same ?
Same formula: $F_r$ is the sum of a positive and a negative part ?

And where does $F_x = 0.6*700*9.81$ N come from ? You sure it applies ?

 

[BvU]

$\omega$ should the sam direction as torque

I don't see $\omega$ appearing anywhere.

 

[Payam30]

I agree. So is -550.
But, just like the other numbers, to me they come out of the blue sky.

If they come from your second relevant formula, however, they are definitiely wrong: there is no way a momentum and a force can be equal. They simply don't have the same dimension. What is it you mean to say with $m \dot{v} = F_x + F_r$ ?

[edit]Sorry, missed the dot.

In your first formula you write $T$ and $F_x\,R_e$ on one side with opposite signs. You sure this is the equation of motion ? Aren't $T$ and $F_x\,R_e$ one and the same ?
Same formula: $F_r$ is the sum of a positive and a negative part ?

And where does $F_x = 0.6*700*9.81$ N come from ? You sure it applies ?

Now I'm confused, look at the reference here.
https://theses.lib.vt.edu/theses/available/etd-5440202339731121/unrestricted/CHAP3_DOC.pdf
From the figure and in order to have balance you have to have a $T$ and #Fx# is the traction force that is a function of $\mu$ that is the friction coefficient that is in turn a function of longitudinal slip $\lambda$. No we consider $\mu$ to be constant. $F_r$ is rolling resistance force. The refence above in page 35 eliminates $F_r$ by some reason. According to https://link.springer.com/chapter/10.1007/0-387-28823-6_4 $F_r$ does not give any moment about wheel centrum and is acting on the centrum of tire. but on EOM (equation of motion) it is considered negative. but it contradicts the first reference wher equation of interia and angular acceleration states the contribution of Fr is $-F_R *R_e$ thus $F_r$ and $F_x$ should in same direction.

$\mu = 0.6$ and $m = 700$ and $J=25.1$ is assumed. $F_x = 0.6*700*9.81=\mu*g*m$ where $g = 9.81$.

 

[jack action]

When I try to solve for ω for this system

How can you do that? $\omega$ and $v$ have nothing to do with your equations. The equations only (correctly) consider accelerations. They can be true at any value of $\omega$.

 

[Payam30]

How can you do that? $\omega$ and $v$ have nothing to do with your equations. The equations only (correctly) consider accelerations. They can be true at any value of $\omega$.

I only integrate the \dot{\omega}. can you explain more. Do you think negative values of $\omega$ are okej? I tried with higher torque and it worked. The problem is Matlab or any programming language doesn't know where it exists any forces. For example when the vehicle is standing still, there arent any forces or if that is they have to lead to a stationary state.

 

[jack action]

Show us the equations and the values used for integration then. Your equations for force and acceleration are good.

Of course, negative values are acceptable. For example, if the input torque is zero and you have a headwind, the wheel will back up and you will have a negative velocity. I suspect the answer to your problem lies in the values (limits and conditions) you used with your integration, more than your equations themselves.