Equations of Motion Homework: Acceleration of Block A

[aaronfue]

Homework Statement

I seem to be having trouble setting up my equations and not getting the correct answer to some of these problems.

Ex 1:
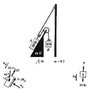
Determine the acceleration of block A when the system is released. The coefficient of friction and the weight of each block are indicated in the figure. Neglect the mass of the pulleys and cords. See attached image.

Homework Equations

m = \frac{lb}{32.2}

So for my first set of equations on block A:
ƩF_x = 2T+ μmgcos60° - mgsin60° = (\frac{lb}{32.2})a_A

ƩF_y = N - mgcos60° = 0
N = mgcos60°

F_f = μ*N = μmgcos60°

Block B:
+\uparrow
ƩF_y = T - mg = (\frac{lb}{32.2})a_B

Pulley:
a_B = -2a_A

1. Are my equations correct?
2. Was I correct to use 60°? (I'm sure it is right but...I feel a bit doubtful.)

 

[ehild]

Look at the picture. The angle is 30°.

ehild