Dilemma
- 15
- 1
Hello,
Circuit:
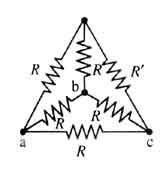
1. Homework Statement
Determine the net resistance between points a and c and a and b. Assume R' ≠ R.
ε - IR = 0
V = IR
http://i.imgur.com/Y2KPI20.jpg
I applied an emf between the points a and c, and tried to solve using Kirchhoff's rules. The question suggests me to use symmetry at junctions but I can not see any.
Thanks in advance.
Circuit:
1. Homework Statement
Determine the net resistance between points a and c and a and b. Assume R' ≠ R.
Homework Equations
ε - IR = 0
V = IR
The Attempt at a Solution
http://i.imgur.com/Y2KPI20.jpg
I applied an emf between the points a and c, and tried to solve using Kirchhoff's rules. The question suggests me to use symmetry at junctions but I can not see any.
Thanks in advance.
 ,
,