Equilibrium and tension problem

[FarazAli]

The problem as stated in the book
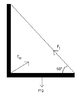
"Calculate the tension F_{t} in the wire that supports the 30-kg beam shown in fig. 9-57 (attached), and the force F_{w} exerted by the wall on the beam (give magnitude and direction)."

Getting the Tension in the string was easy.
\sum\tau = F_{ty} \cdot x_{1} - mg(\frac{x_{1}}{2}) = 0
F_{ty} = 147N
F_{t} = \frac{F_{ty}}{sin 50} = 1.9 \times 10^2N

To get the F_{w}, I used the sum of forces.
\sum{F_{x}} = F_{tx} - F_{wx} = 0 \Rightarrow F_{tx} = F_{wx} = F_{t} \cdot cos 50 = 123.35 N
\sum{F_{y}} = F_{ty} + F_{wy} - mg \Rightarrow F_{wy} = mg - F_{ty} = 102.11 N

So now I have the two components for F_{w} , I use pythagorous and solve for the resultant vector to get 160.13 N. The book, however, says the answer is 1.9 \times 10^2 N. Can anyone tell me what I'm doing wrong?

 

[FarazAli]

nevermind, the problem was when I confused F_{wy} for F_{w}

 

[wais]

In this problem, you are trying to find the tension in the wire and the force exerted by the wall on the beam. The equation you used to find the tension in the wire (F_{ty} = 147N) is correct. However, when finding the force exerted by the wall, you made a mistake in your calculation.

To find the force exerted by the wall, you need to use the equation \sum{F_{y}} = F_{ty} + F_{wy} - mg. This equation takes into account the weight of the beam (mg) and the tension in the wire (F_{ty}). So the correct equation would be F_{wy} = mg - F_{ty} = 102.11 N. This means that the force exerted by the wall is actually 102.11 N, not 160.13 N as you calculated.

To understand why your calculation was incorrect, you need to think about the forces acting on the beam. The weight of the beam is pulling down with a force of mg, and the tension in the wire is pulling up with a force of F_{ty}. The force exerted by the wall must balance out these two forces, which means it must be equal in magnitude but in the opposite direction. So, when you used the equation \sum{F_{y}} = F_{ty} + F_{wy} - mg, you were essentially adding the weight of the beam twice, which resulted in the incorrect value of 160.13 N for the force exerted by the wall.

In conclusion, to find the force exerted by the wall, you need to use the correct equation and take into account the weight of the beam. Your calculation for the tension in the wire is correct, but your calculation for the force exerted by the wall was incorrect due to a mistake in the equation used.