Equivalent Capacitance of a network

[Canopuswr]

Homework Statement

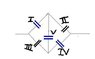
To find the equivalent capacitance of the following network (image attached at the end of the post). The blue capacitors have capacitance of 2C and the black ones have a capacitance of C.

Homework Equations

Q = CV where Q is the charge on a capacitor, C it's capacitance and V the potential difference through it's terminals.
Q_t=C'*V_n, where Qt is the total charge stored by the network (I need help with this, I think Qt is the charge on capacitor 1 + the charge on capacitor 3, but I am not sure), Vn the potential difference across the network and C' the equivalent capacitance, which is what I'm seeking
\frac{1}{C'} = \frac{1}{C_1}+\frac{1}{C_2}+...+\frac{1}{C_n} for the equivalent capacitance C' of n capacitors in series
C' = C_1+C_2+...+C_n for the equivalent capacitance of n capacitors in parallel
\sum_{i=0}^n\ V_i = 0
if Vi is the voltage across the capacitors and if you follow them in a loop (also being a little careful with signs) (this is the same as closed loop integral of E*dl = 0)

The Attempt at a Solution

Not much of an attempt, since it needs some more before i might get something valid from it, but, not knowing how to do it just with series/parallel, I'm doing it using what I know about charges on the plates and potentials. going through the capacitors in loops i get
V_I+V_I_I=V_I_I_I+V_I_V
V_I+V_V=V_I_I_I
V_V+V_I_V=V_I_I
I was thinking of using the fact that the charges on the "inner plates" need to add up to zero in order for charge to be conserved (no charge moves through the capacitors), but I'm not sure on which side will Capacitor V have postive charge and on which side it will have negative charge (this changes the result, I think) and I'm assuming all the other capacitors will have postive charge on their "left" plate and negative on the "right" plate (I'm solving this from right to left, even though it's symmetric that way).
Assuming Capacitor V has positive charge on the upper plate, i think the equations should be
2CV_I=2CV_V+CV_I_I
CV_I_I_I=-2CV_V+2CV_I_V

And that would completely determine the problem (the system is to have infinitely many solutions), since I can find the charge on capacitors 1 and 3, their sum (I think) being Qt and I can add potential differences V1 and V2 to get the potential difference across the network and that's that. I am however shaky on the last two equations and I don't know if the Qt is the sum of charges on capacitors 1 and 3.
I appreciate the help.

 

[Canopuswr]

Oh god, I'm sorry, i forgot to attach the file. there it is.