JasonHathaway
- 113
- 0
Homework Statement
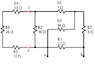
Determine the equivalent resistance Req as seen by the voltage source VS (the resistance between a and b)
http://i.imgur.com/A1ueQnd.jpg
Homework Equations
Series-Parallel combinations
The Attempt at a Solution
http://i.imgur.com/K1ItpF0.jpg
The only resistor that have both a and b on its terminals is R2 (12 ohms)
So, is Req=R2=12 ohms?