WhiskeyHammer
- 8
- 0
I have an equation that I've been trying to solve. I manipulated it until I had a=f(d) and then did by best to put it into a format the computer recognizes. However when I went back to check the results against the unsimplified version of the equation, they didn't work out as they should have; which tells me I screwed up manipulating the equation to a=f(d) or when I translated it from paper to program*. Im stumped.
If someone could take a look at my work for errors Id appreciate the second set of eyes.
Algebraic Manipulation:
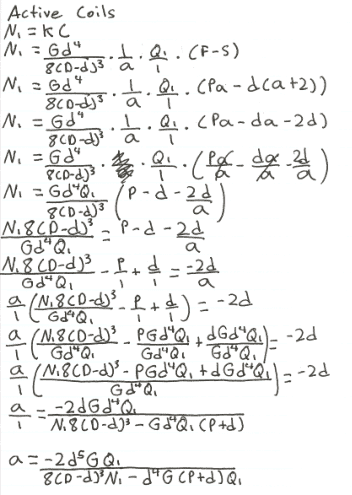
Im fairly certain of my work until the fourth line, but if you need to see how I got there let me know.
Computational Form:
a=((-2)(x^5)(G)(q))/(((8)((D-x)^3)(n))-((G)(x^4)(q)(((tan(12))(pi)(D-x))+x)))
This is where I feel like the problem might be. I am relatively inexperienced using long equations in a computer setting.
*the third possibility being that I messed up checking the equation, but it seemed more prudent to start here
If someone could take a look at my work for errors Id appreciate the second set of eyes.
Algebraic Manipulation:
Im fairly certain of my work until the fourth line, but if you need to see how I got there let me know.
Computational Form:
a=((-2)(x^5)(G)(q))/(((8)((D-x)^3)(n))-((G)(x^4)(q)(((tan(12))(pi)(D-x))+x)))
This is where I feel like the problem might be. I am relatively inexperienced using long equations in a computer setting.
*the third possibility being that I messed up checking the equation, but it seemed more prudent to start here