john325
- 5
- 0
Thread moved from the technical forums to the schoolwork forums
TL;DR Summary: Trying to understand why there might be errors when using certain materials in a physics lab and how aluminum foil might impact this.
I am looking for assistance on answer these questions.
1) What would likely be a significant source of error in performing this experiment on other materials that have very low thermal conductivities that you would not see for materials that have higher thermal conductivities?
2) What would likely be a significant source of error in performing this experiment on other materials that have very high thermal conductivity that you would not see for materials that have lower thermal conductivities?
and
3) Would there be any advantage to wrapping the Plexiglass and glass samples in aluminum foil like the pine and sheet rock were?
I have been thinking if with a very low conductivity material if that much of the heat is lost by convection, because convection would work quicker on the ice versus conduction. I am not sure if this is an accurate statement. As for a material with very high conductivity, would errors arise in the rapid warming of the ice? How so? Also, for number 3, I am under the assumption that because Plexiglass and glass samples have high conductivities already, if aluminum foil would not offer an advantage but act as an insulator. I have attached the lab set up.
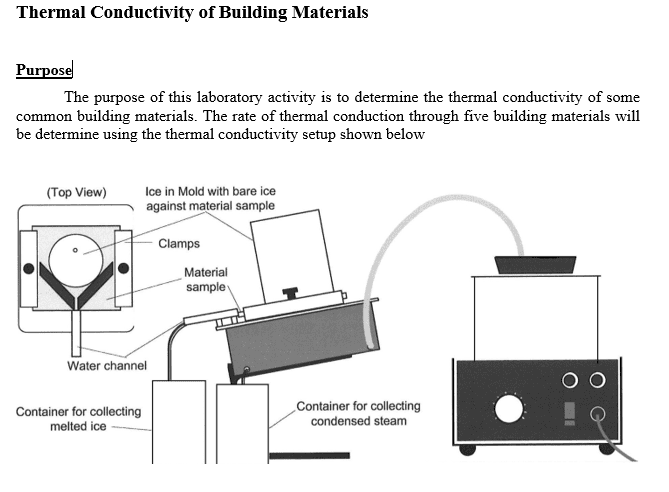
I am looking for assistance on answer these questions.
1) What would likely be a significant source of error in performing this experiment on other materials that have very low thermal conductivities that you would not see for materials that have higher thermal conductivities?
2) What would likely be a significant source of error in performing this experiment on other materials that have very high thermal conductivity that you would not see for materials that have lower thermal conductivities?
and
3) Would there be any advantage to wrapping the Plexiglass and glass samples in aluminum foil like the pine and sheet rock were?
I have been thinking if with a very low conductivity material if that much of the heat is lost by convection, because convection would work quicker on the ice versus conduction. I am not sure if this is an accurate statement. As for a material with very high conductivity, would errors arise in the rapid warming of the ice? How so? Also, for number 3, I am under the assumption that because Plexiglass and glass samples have high conductivities already, if aluminum foil would not offer an advantage but act as an insulator. I have attached the lab set up.
Attachments
Last edited by a moderator:
