nmego12345
- 21
- 0
So I was reading this book, "Euclidean and non Euclidean geometries" by Greenberg
I solved the first problems of the first chapter, and I would like to verify my solutions
1. Homework Statement

[/B]
Um, none that I can think of?
(1) Correct
(2) It is defined as: "An "angle with vertex A" is a point A together with two distinct nonopposite rays AB and AC (called the sides of the angle) emanating from A
We're asked if it is defined as the space between two rays that emanate from a common point
I think that's incorrect
(3) Incorrect
(4) Incorrect (2 lines are parallel if they don't intersect)
(5) Incorrect (it wasn't proven)
(6) Correct
(7) Incorrect (it is a right angle if it has a supplementary angle to it to which it is congruent
(8) Correct
(9) Correct
(10) Correct
Definitions:
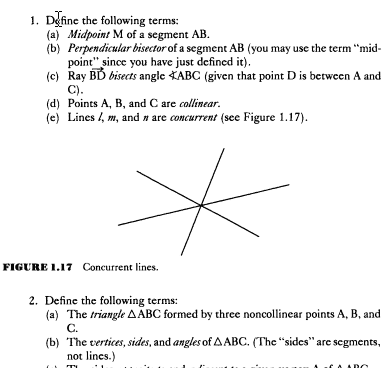
1. (a) Midpoint M of a segment AB
M is the midpoint of the segment AB if M lies on segment AB where the segment MA is congruent to the segment MB
1. (b) Perpendicular bisector of a segment AB
l is the Perpendicular bisector of the segment AB if the line l is perpendicular to line AB (we've already defined that two lines (l, m) are perpendicular if they intersect at a point A and if there is a ray AC that is part of l and a ray AC that is part of M such that angle BAC is right angle) and if the point of intersection of the lines l and AB is also the midpoint of the segment AB
1. (c) Ray BD bisects angle ABC if angle ABD is congruent to the angle CBD
1. (d) Points A, B, and C are collinear, if the rays BA and BC are opposite
1. (e) lines l, m and n are concurrent if the lines l and m intersect at a point A and the lines m and n intersect at point A as well
2.(a) The triangle ABC formed by three collinear points A, B and C is the set of points that lie on the segment AB + the set of points that lie on the segment BC + the set of points that lie on the segment CA
2.(b) The vertices of ABC are the three points that lie on the triangle ABC in which if we draw line segments joining the 3 of them, we'll get a triangle congruent to triangle ABC
The sides of ABC are the 3 segments that lies on the triangle ABC where the first and second segment intersect at the first vertex, the second and third segment intersect at the second vertex, and the third and first segment intersect at the third vertex
The angles of ABC are the 3 angles in which each angle is formed of the union of a vertex of tirangle and the 2 rays that emanate from that vertex in which the two sides that intersect at the vertex each of them is part of one of the 2 rays.
(Should I say that they are called angles ABC, CAB and ACB or I don't have to?)
I want to safecheck my solutions before solving other problems
I solved the first problems of the first chapter, and I would like to verify my solutions
1. Homework Statement
Homework Equations
[/B]
Um, none that I can think of?
The Attempt at a Solution
(1) Correct
(2) It is defined as: "An "angle with vertex A" is a point A together with two distinct nonopposite rays AB and AC (called the sides of the angle) emanating from A
We're asked if it is defined as the space between two rays that emanate from a common point
I think that's incorrect
(3) Incorrect
(4) Incorrect (2 lines are parallel if they don't intersect)
(5) Incorrect (it wasn't proven)
(6) Correct
(7) Incorrect (it is a right angle if it has a supplementary angle to it to which it is congruent
(8) Correct
(9) Correct
(10) Correct
Definitions:
1. (a) Midpoint M of a segment AB
M is the midpoint of the segment AB if M lies on segment AB where the segment MA is congruent to the segment MB
1. (b) Perpendicular bisector of a segment AB
l is the Perpendicular bisector of the segment AB if the line l is perpendicular to line AB (we've already defined that two lines (l, m) are perpendicular if they intersect at a point A and if there is a ray AC that is part of l and a ray AC that is part of M such that angle BAC is right angle) and if the point of intersection of the lines l and AB is also the midpoint of the segment AB
1. (c) Ray BD bisects angle ABC if angle ABD is congruent to the angle CBD
1. (d) Points A, B, and C are collinear, if the rays BA and BC are opposite
1. (e) lines l, m and n are concurrent if the lines l and m intersect at a point A and the lines m and n intersect at point A as well
2.(a) The triangle ABC formed by three collinear points A, B and C is the set of points that lie on the segment AB + the set of points that lie on the segment BC + the set of points that lie on the segment CA
2.(b) The vertices of ABC are the three points that lie on the triangle ABC in which if we draw line segments joining the 3 of them, we'll get a triangle congruent to triangle ABC
The sides of ABC are the 3 segments that lies on the triangle ABC where the first and second segment intersect at the first vertex, the second and third segment intersect at the second vertex, and the third and first segment intersect at the third vertex
The angles of ABC are the 3 angles in which each angle is formed of the union of a vertex of tirangle and the 2 rays that emanate from that vertex in which the two sides that intersect at the vertex each of them is part of one of the 2 rays.
(Should I say that they are called angles ABC, CAB and ACB or I don't have to?)
I want to safecheck my solutions before solving other problems
Last edited: