- #1
David Fishber
- 2
- 0
Hi,
I'm having a problem in evaluating a triple integral for a deformable control volume equation:
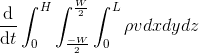
where v is defined as:
![y}{W})^{2}&space;\right&space;]\frac{z}{H}\left&space;(&space;2-\frac{z}{H}&space;\right&space;).gif y}{W})^{2}&space;\right&space;]\frac{z}{H}\left&space;(&space;2-\frac{z}{H}&space;\right&space;).gif](https://www.physicsforums.com/attachments/y-w-2-space-right-space-frac-z-h-left-space-space-2-frac-z-h-space-right-space-gif.139469/)
When I evaluate the triple integral in Maple and by hand I get:
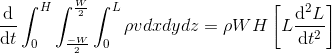
The correct answer is:
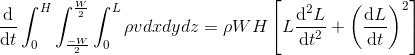
Can someone please explain where the last term on the RHS comes from??
Thanks in advance,
David
I'm having a problem in evaluating a triple integral for a deformable control volume equation:
where v is defined as:
When I evaluate the triple integral in Maple and by hand I get:
The correct answer is:
Can someone please explain where the last term on the RHS comes from??
Thanks in advance,
David