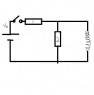
throneoo
- 125
- 2
Homework Statement
(see figure)[/B]
The switch is initially open for a long time.
At t=0 it is closed, and after 1ms it is reopened.
Find the voltage across Resistor 2 at (i)0<t<1ms and (ii) t>1ms.
Homework Equations
V0=120V
R1=500 Ω
R2=125 Ω
Inductance of the inductor = 0.2 H
The Attempt at a Solution
(i)
Taking reference points across the inductor, the Thevenin circuit has applied voltage 24V and resistance 100 Ω.
The inductor tries to oppose the sudden increase in current and generates an emf with voltage
24*exp(-RThevenint/L)24*exp(-100t/0.2)=24*exp(-500t).
Back to the original circuit, by Kirchoffs voltage law, the voltage across Resistor 2 = that of the inductor =24*exp(-500t) V
with an anti-clockwise current
(ii)
At t= 1ms, the voltage across Resistor 2 = 24*exp(-0.5) and the current is (24/125)*exp(-0.5) anticlockwise...
I stopped here due to the following questions.Question:
(i)
Does the applied voltage contribute to the current flowing through Resistor 2 at all? Maybe it does only at the moment the switch is closed, when the inductor behaves like an open circuit by generating 24V to oppose the applied voltage. After this instant, the inductor has no resistance at all and it shorts out Resistor 2.
How can I apply superposition theorem in this problem? How do I isolate the effect of the inductor? Something tells me it's not as simple as replacing it as an open/close circuit because of its time dependent behavior. This concerns how I find the current in each circuit element as a function of time.
(ii)
When the switch is reopened, does the transient response from the closing of the switch still remain?
If that is the case , there would be a superposition of response across the inductor/resistor.
Otherwise, the new response would still have to counteract the current from Resistor 2 and the absence of the voltage source.
But how do I find the new response?
The inductor would produce a voltage to maintain the initial current across it, which is 0.24*(1-exp(-0.5)) (downward/clockwise) but what's next?