- 2,076
- 140
Homework Statement
Been awhile since I looked at this, just seeing if I still know what I'm doing here.
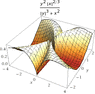
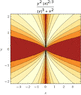
Suppose : f(x,y) = \frac{x^{2/3}y^2}{x^2 + |y|^3} for (x,y) ≠ (0,0).
1. Show that on every straight line through the origin the limit as (x,y) → (0,0) of f(x,y) exists.
2. Does the general limit as (x,y) → (0,0) exist? Justify!
Homework Equations
I'm thinking I might need a formal epsilon delta proof for part 2.
The Attempt at a Solution
1. So every straight line through the origin means that I want to consider y = mx.
f(x, mx) = \frac{m^2x^{8/3}}{x^2 + |mx|^3}
Now, I have sadly forgotten what I must do here. I know I want to take the limit as x goes to zero, but my brain is having a hiccup for some reason doing the algebra. Should I divide through by x3 like I'm thinking or?
2. I'm quite certain that this limit is not going to exist in general. Not sure how to go abouts it yet though.
Thanks for any help in advance :).