- #1
Fluorine
Homework Statement
[/B]
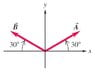
Sketch in a third vector, C, whose magnitude and direction are such that A+B+C=0. Vectors A and B both have a magnitude of 5 and form a 30 degree angle (image attached).
Homework Equations
[/B]
How do I go about this question? I have no idea how to start or what to graph.
The Attempt at a Solution
[/B]
Haven't been able to attempt anything yet because I don't know how to start this problem.