Expressing current through a circuit

[Ozmahn]

Homework Statement

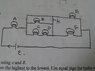
Six identical light bulbs (A-F) are connected in the following circuit. The resistance of each bulb is R and the idealistic battery has an emf of E. The switch K remains open (not connected) for questions (a) through (c).

https://mail.google.com/mail/u/0/?ui=2&ik=bc505e9c61&view=fimg&th=14d778cdba4f2ea7&attid=0.1&disp=inline&realattid=1501801808870244352-local0&safe=1&attbid=ANGjdJ_jML1j_uxhOOejtQqrl6EizyxYtYjk-AO81psFg2w8clQTt8C-cGlvgZ2H049s4UYhNnWwWph-RWZ5dgCDVC0ZsduDmthKvAT4lWWMo8iGGe23ryb7qEsBK1E&ats=1432229831281&rm=14d778cdba4f2ea7&zw&sz=w1342-h523

(a) Express the current through the battery using E and R.

(b) solved

(c) Rank the brightness of the bulbs from the highest to the lowest.

(d) Now the switch K is closed (connected). Which bulbs go off as a result?

Homework Equations

Resistors in series
R1+R2+...=Req

Resistors in parallel
1/R1+1/R2+...=1/Req

V=IR

The Attempt at a Solution

(a)
C and D are in series
R+R=2R
CD parallel to B
1/2R+1/R=3/2R=>2R/3
BCD and A in series
2R/3+R=5R/3
ABCD and F are in series
5R/3+R=8R/3
ABCDF and E are parallel
3/8R+1/R=11/8R=>8R/11=Req

V=IR => I=V/R, where V is the emf (E)
I=E/8R/11 => 11E/8R

This is what I got as the answer, but the solution shows that instead of combining ABCD and F, you combine ABCD and E first, then ABCDE and F. I worked it out that way and got 8E/13R, but I'm not seeing any reason why you would combine the resistors in that order. Why would the order in which you combine these matter?

(c) Okay so I know that A must be the brightest since it is getting the full current (E/R), but the other ones I'm not as sure about. C and D should be getting the same, since they are in series in the same branch. And B should get twice as much as C or D, so IC+ID=IB. I'm assuming E is the second brightest because there are no resistors between it and A. So then F would be third, since the current flowing through the CD and B branches would be split between that and E...that's my rationale anyway. So the answer is:

A>E>F>B>C=D

It's a bit confusing to be honest, and I used the solution to come up with that explanation. Is there an easier way to determine this?

(d) The solution says that BCD are turned off when the switch is closed. Would this be because there is zero resistance along the wire that bypasses those branches, so the current follows the wire with least resistance? Just a wild guess on that one.

Any help/clarification for these problems is greatly appreciated. Thank you!

EDIT: The problem didn't show up in the threa, so I attached it as a jpg file.

 

[cpscdave]

This is what I got as the answer, but the solution shows that instead of combining ABCD and F, you combine ABCD and E first, then ABCDE and F. I worked it out that way and got 8E/13R, but I'm not seeing any reason why you would combine the resistors in that order. Why would the order in which you combine these matter?

Try re-drawing the circuit, and you'll see that this does make sense. Perhaps when you understand part D it'll help

(d) The solution says that BCD are turned off when the switch is closed. Would this be because there is zero resistance along the wire that bypasses those branches, so the current follows the wire with least resistance? Just a wild guess on that one.

Any help/clarification for these problems is greatly appreciated. Thank you!

If that switch is closed, what is the Potential at the branch after A and the potential on the wire that connects B to CD? Remember when doing these circuits if you can trace a path between 2 points with no resistors they'll be at the same potential

 

[Hesch]

(a)
C and D are in series
R+R=2R
CD parallel to B
1/2R+1/R=3/2R=>2R/3
BCD and A in series ( F is in series with BCD, you must find BCDF, then BCDFE, then ABCDFE )
2R/3+R=5R/3
ABCD and F are in series
5R/3+R=8R/3
ABCDF and E are parallel
3/8R+1/R=11/8R=>8R/11=Req

See the correction in the quote.

 

[Ozmahn]

That makes a lot of sense, thank you both!