Hepth said:
Do you have that equation in Input form so I can play with it?
Here you go:
{1, x, y, x^2, y^2, xy, x^3, x^2 y, xy^2,
y^3}.{{Subscript[q, 11], Subscript[q, 12], Subscript[q, 13],
Subscript[q, 14], Subscript[q, 15], Subscript[q, 16],
Subscript[q, 17], Subscript[q, 18], Subscript[q, 19],
Subscript[q, 110]},
{Subscript[q, 12], Subscript[q, 22], Subscript[q, 23],
Subscript[q, 24], Subscript[q, 25], Subscript[q, 26],
Subscript[q, 27], Subscript[q, 28], Subscript[q, 29],
Subscript[q, 210]},
{Subscript[q, 13], Subscript[q, 23], Subscript[q, 33],
Subscript[q, 34], Subscript[q, 35], Subscript[q, 36],
Subscript[q, 37], Subscript[q, 38], Subscript[q, 39],
Subscript[q, 310]},
{Subscript[q, 14], Subscript[q, 24], Subscript[q, 34],
Subscript[q, 44], Subscript[q, 45], Subscript[q, 46],
Subscript[q, 47], Subscript[q, 48], Subscript[q, 49],
Subscript[q, 410]},
{Subscript[q, 15], Subscript[q, 25], Subscript[q, 35],
Subscript[q, 45], Subscript[q, 55], Subscript[q, 56],
Subscript[q, 57], Subscript[q, 58], Subscript[q, 59],
Subscript[q, 510]},
{Subscript[q, 16], Subscript[q, 26], Subscript[q, 36],
Subscript[q, 46], Subscript[q, 56], Subscript[q, 66],
Subscript[q, 67], Subscript[q, 68], Subscript[q, 69],
Subscript[q, 610]},
{Subscript[q, 17], Subscript[q, 27], Subscript[q, 37],
Subscript[q, 47], Subscript[q, 57], Subscript[q, 67],
Subscript[q, 77], Subscript[q, 78], Subscript[q, 79],
Subscript[q, 710]},
{Subscript[q, 18], Subscript[q, 28], Subscript[q, 38],
Subscript[q, 48], Subscript[q, 58], Subscript[q, 68],
Subscript[q, 78], Subscript[q, 88], Subscript[q, 89],
Subscript[q, 810]},
{Subscript[q, 19], Subscript[q, 29], Subscript[q, 39],
Subscript[q, 49], Subscript[q, 59], Subscript[q, 69],
Subscript[q, 79], Subscript[q, 89], Subscript[q, 99],
Subscript[q, 910]},
{Subscript[q, 110], Subscript[q, 210], Subscript[q, 310],
Subscript[q, 410], Subscript[q, 510], Subscript[q, 610],
Subscript[q, 710], Subscript[q, 810], Subscript[q, 910],
Subscript[q,
1010]}} .{{1}, {x}, {y}, {x^2}, {y^2}, {xy}, {x^3}, {x^2 y},
{xy^2}, {y^3}}
Hepth said:
Also, have you tried just Expand[%]?
Unfortunately, I've tried it without success.
Thanks for the help!
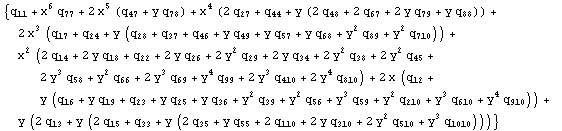 and using Mathematica 7 I want to factor out terms such as x,y,xy, x^2y,xy^2, etc. so that I'll have it in a form similar to
and using Mathematica 7 I want to factor out terms such as x,y,xy, x^2y,xy^2, etc. so that I'll have it in a form similar to